Module 8: Loops

Lesson 8.1 – while Loops

Learning Objectives

After reading this lesson, you should be able to:

• differentiate between a definite and an indefinite loop,

• write programs using while (indefinite) loops with one condition,

• write programs using while loops with multiple conditions.

In all the previous lessons, we have considered two basic control structures: sequence and conditional. In this lesson, we introduce you to the control structure of repetition (or “loops”).

What is a loop?

In programming, a loop is a syntax used to describe the action of repeating a block of code (task) more than once. This block of code (task) is commonly referred to as the body of the loop. In Figure 1, we can see two equivalent representations of code. On the left side, the same block of code is repeated multiple times explicitly, while a loop is used on the right side.

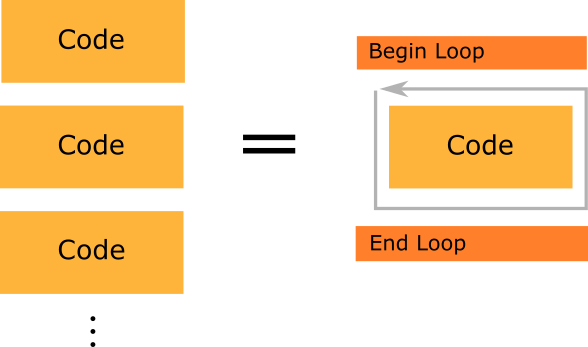
Figure 1:  The fundamental structure of loops is to run the same block of code many times.

There are two types of loops: the for loop and the while loop. The for loop will conduct a task a definite number of times because its repetition is controlled by a counter, whereas the while loop will perform a process an indefinite (not to be confused with an infinite) number of times because its repetition is controlled by a logical expression. We will cover while loops in this lesson and for loops in Lesson 8.2.

What is a while loop?

The while loop conducts an indefinite number of repetitions (loops), where the number of repetitions is controlled by a conditional expression. The while loop will continue to conduct repetitions until the conditional expression becomes false. Once the conditional expression is false, MATLAB exits the while loop and continues to execute the m-file from the lines below the loop end statement. The four main components of a while loop are

1. the statement (while),

2. conditional expression,

3. the body of the loop,

4. end statement.

The conditional expression(s) used in the while loop are the same type of comparisons (for example, >, <=, ~=) and logical operators (for example, ||, &&) used in if statements.

When programming with while loops, one must be careful to avoid an infinite loop. Remember, the loop will continue to run until the conditional expression is false. If you find yourself in an infinite loop (where the conditional expression never becomes false) in MATLAB, simply click inside the Command Window and hit Ctrl+c to end the execution of the program. However, if you have pressed “run” multiple times, you will need to repeat the stop command (Ctrl+c) multiple times.

Important Note: Be careful of infinite loops! An infinite loop is when you write a condition that is always true and never becomes false. For example, while 1 \> 0.

Example 1

Output the square of all the integers from 3 to 7 in the Command Window. If one wants to write out the square of the integers from 3 to 7, one can write a MATLAB code for it as follows:

 

i = 3;

fprintf(\'Square of %g is %g\', i, i\^2)

i = 4;

fprintf(\'Square of %g is %g\', i, i\^2)

i = 5;

fprintf(\'Square of %g is %g\', i, i\^2)

i = 6;

fprintf(\'Square of %g is %g\', i, i\^2)

i = 7;

fprintf(\'Square of %g is %g\', i, i\^2)

 
As one can see in the above code, the only thing changing in each line is the value of i (also compare with Figure 1). Now take the case where one has to find the squares of numbers from 3 to 100, you will have a lot of code to write. This is a good example of showing the need for a loop.

Solution

Now, we will solve the problem using a while loop. Notice that a pseudocode is first made to help identify what variables are changing and what expressions to display. When programming with loops, you may be tempted to jump in with both feet, but you need to clearly identify which variable(s) are changing, and which segments of program are repetitive.

Pseudocode for Example 1:

1. Start program, clear window/variables.

2. Set up a loop to find the square of numbers

\(\;\;\;\;\;\;\;\;\;\ \) Starting number = 3

\(\;\;\;\;\;\;\;\;\;\ \) Final number = 7

\(\;\;\;\;\;\;\;\;\;\ \) Increment by 1

\(\;\;\;\;\;\;\;\;\;\ \) Square each number.

3. Display output

4. End loop when final number is reached

5. End program

Remember, all loops must be terminated with an end statement.

In Example 1, the value of i is changing. The while loop starts with the value of i being 3, and then increments the value of i by 1 until the loop completes with the value of i being 7. There are multiple correct solutions for the while-end loop in Example 1 – one could change the condition of the while statement and the placement of the incrementing line (i = i + increment). For example, another correct solution could include the while loop condition as i \< endNum. Consider what else would need to be changed to get the same output as shown in the Command Window Output. Doing exercises like this will be helpful when solving more complex problems with loops because it will deepen your understanding of the fundamentals.

Example 2

Using a while loop, write a program that counts to four. The counting should be displayed in the Command Window.

Solution

The iterator, i, is what counts for us in the solution. We can name the iterator any valid variable name (other examples for this case are num or count).

It is essential to understand that the condition for the while loop can be anything that fits your problem and does not make the while loop infinite. Although the examples we have seen so far have while loops that solely rely on a counter variable for their conditions, there are other common examples that have distinctly different conditions. Some informal examples of this are:

1. Let us say you have a case where an engineer wants to gather sensor data. We might want to write a program using a while loop that stops based on user input.

stop = false;

while stop == false

%Code to get sensor reading

end

2. In Example 3, we want to calculate values of a function over a specific range: so we use a counter (the independent variable, \(x\)) in the condition. However, we might, instead, want to stop the loop when \(y(x)\) becomes negative or reaches a specific value. In these instances, we would write our condition with those in mind rather than the counter (iterated variable).

Example 3

Given \(y(x) = x^2 - 49\), display the value of \(y\) only when \(y\) is positive for \(x = -10, -9,\ ...\ 9, 10\).

Solution

Pseudocode for this example:

1. Clear Command Window and all workspace variables.

2. Initialize the starting value of x

\(\;\;\;\;\;\;\;\;\;\ \) starting point is -10

3. Conduct loop repetitions while true.

\(\;\;\;\;\;\;\;\;\;\ \) number, x less than or equal to 10

4. Loop body:

\(\;\;\;\;\;\;\;\;\;\ \) Conduct, \(y = x ^2 - 49\)

\(\;\;\;\;\;\;\;\;\;\ \) Place logic test: is y > 0?

\(\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\ \) If true, display y

\(\;\;\;\;\;\;\;\;\;\ \) Increase count by one

5. End loop

The Command Window for Example 3 shows that although the while loop is continuing to run for all integer values of \(x\) from -10 to 10 as we required; a conditional statement inside of the loop ensures that only positive values of \(y\) are displayed in the Command Window.

Example 4

Write a while loop to find the value of \(x\) which is updated recursively by

\[\frac{1}{2}\left ( x + \frac{9}{x} \right )\]

Use a starting value of \(x = 64\) and do the recursion 10 times. Display the last updated value of \(x\) as the only output.

Solution

Pseudocode for this example:

1. Clear Command Window and all workspace variables.

2. Initialize loop count, starting at 1.

3. Continue loop while true:

\(\;\;\;\;\;\;\;\;\;\ \) While count is less than or equal to 10

4. Body of loop:

\(\;\;\;\;\;\;\;\;\;\ x = (1/2)*(x+(9/x))\)

5. Display last updated value of x

6. End loop

The program increases the loop counter, i, by one for each repetition. Once the loop counter, i, is greater than 10, the while loop conditional expression is false and the loop terminates. Observing precisely how loops work from one iteration to the next is essential to being successful in this module.

To give you a background of the above example from a practical point of view, the recursive formula is a way to find the square root of 9. In fact, you can find the square root of any positive real number R by using the recursive formula

\[x_{i+1} = \frac{1}{2}\left ( x_{i} + \frac{R}{x_{i}} \right )\]

What comparisons can I use with a while loop?

The comparisons used with the while loop are the same as those used for conditional statements (if statements). These are shown in Table 1. Just like in conditional statements, you may make more than one comparison in the while loop. You can join each comparison by using the && (AND) and || (OR) operators.

Table 1: Operators to be used for while loop comparison.

Meaning	Code
Greater than	>
Greater than or equal to	>=
Less than	<
Less than or equal to	<=
Equal to	==
Not equal to	~=
Boolean Operators
AND	&&
OR	||

The while loop is an indefinite loop, and hence we need to be careful as to not let it become an infinite loop! For instance, in Example 5, if the series does not converge, you will have yourself an infinite loop. To prevent this from happening, we add a condition to the while loop that limits the maximum number of terms added to the series, maxTerms. As soon as the number of terms used, term, becomes greater than the maximum number of terms allowed, maxTerms, the loop condition will not be met, and thus the loop will end.

The value of the exponential function, \(e^x\), can be found by the following series

\[e^{x} = 1 + x + \frac{x^{2}}{2!} + \frac{x^{3}}{3!} + ... + \frac{x^{n}}{n!}\]

Write a program that uses a while loop to find the value of \(e^x\). Define value of \(x\) and stop the loop once the absolute relative approximate error is less than 0.1%. The definition of the absolute relative approximate error is

\[\text{Absolute Relative Approximate Error} = \frac{\left| \text{Previous}\text{ Approximation} -\text{ Present Approximation} \right|}{\left| \text{Present Approximation} \right|} \times {100\ \%}\]

Example 5

Test your program for \(x = 0.75\). Display the final approximation for \(e^x\), the number of terms used, and the last absolute relative approximate error calculated.

Solution

First, one must establish what the inputs are:

1. the number to be evaluated, x,

2. the desired absolute relative error (also called pre-specified tolerance), tolerance.

Now, we define the outputs as:

1. value of \(e^x\), exp1, and,

2. absolute relative approximate error, ARAE,

3. number of terms used, term.

The series expression for \(e^x\) can be rewritten as

\[e^{x} = \frac{x^{0}}{0!} + \frac{x^{1}}{1!} + \frac{x^{2}}{2!} + \frac{x^{3}}{3!} + ... + \frac{x^{n}}{n!} + ...\]

and hence in the compact mathematical form as

\[{e}^{{x}} = \sum_{{i}{=0}}^{\infty}{\ \frac{{x}^{{i}}}{{i}{!}}}\]

Example 5 shows how a while loop can be implemented to find the value of a series within a pre-specified tolerance. Because we need to keep adding terms until the pre-specified tolerance is met, the number of terms to be used is not pre-determined, which is why we use an indefinite loop. It should be noted that as one decreases the pre-specified tolerance, more terms may need to be added to achieve the same level of accuracy. Note that we initialize the absolute relative approximate error, ARAE, as a number bigger than the pre-specified tolerance, tolerance, by adding 1 to it. This is done to get the while loop to start the first time around.

Lesson Summary

Task	Syntax	Example Usage
Iterate over a block of code indefinitely	while	a=0; while a<5; a=a+1; disp(a); end

Multiple Choice Quiz

Problem Set

(1). Write a program using while loop that adds the number 7 to each value of j, as j takes on integer values of 1,2,…,11,12. Output all 12 values to the Command Window.

(2). Write a program using while loop that adds the number 7 to each value of j, as j takes on integer values of 12,11,…,2,1. Output all 12 values to the Command Window.

(3). Using a while loop, write a program that adds together all integers from –20 to 20.

(4). Using a while loop, write a program that outputs cos(x) values until cos(x) changes to a negative number. Take values of x from 0 to \(2\pi\) in increments of 0.1.

(5).Using a while loop, write a program that adds together the elements of any sized vector. Test and run your program using the vector vec = \[2 5 8 -4 7 0 -9\].

(6). Write a MATLAB program that conducts the following summation

\[\text{sum1} = 2 + 3 + 4 + ... + \left( n + 1 \right)\]

where,

n is the number of terms used.

Use the while loop to perform the summation of the first 16 terms.

(7). Using your knowledge of the while loop and conditional statements, write a MATLAB program that determines the value of the following infinite series

\[f\left( x \right) = \frac{1}{2}x + \frac{1}{4}x^{2} + \frac{1}{2}x^{3} + \frac{1}{4}x^{4}\text{....}\]

There are two program inputs, which are,

1. the value of x, and

2. the number of terms to use.

There is one program output, which is

1. the numeric value of the series.

Your program must work for any set of inputs. You may assume that the value for the number of terms to use will always be entered as a positive whole number.

Test your program for the following set of inputs:

number of terms = 32

value of x = 0.46

(8).The function, cos(x) can be calculated by using the following infinite Maclaurin series

\[\cos(x) = 1 - \frac{x^{2}}{2!} + \frac{x^{4}}{4!} - \frac{x^{6}}{6!} + ....\]

The absolute percentage relative approximate error, \(|\varepsilon_{a}|\) is defined as

\(|\varepsilon_{a}| = \left| \frac{\text{Present\ Approximation} - \text{Previous\ Approximation}}{\text{Present\ Approximation}} \right| \times 100.0\)_.

Complete the following.

1. Write the pseudocode for a function that finds the approximate value of cos(x). The function inputs are the argument, x, a pre-specified error tolerance, tol, and a maximum number of terms to use nmax. There are two ways that the loop could end: either it meets the pre-specified tolerance or it uses the maximum number of terms allowed.

2. Write a MATLAB function, myCos, using while loops for calculating cos(x). The stopping criterion is if a pre-specified tolerance is met or if a specified number of terms are used.

The function inputs are

1. the value at which cos(x) needs to be calculated, x,

2. pre-specified tolerance, tol,

3. the maximum number of terms allowed, nmax.

The function outputs are

1. the value of cos(x) when either the maximum number of terms are used or the pre-specified tolerance is met, cosVal,

2. last absolute relative approximate error calculated, absApproxError,

3. the number of terms used, terms, and

4. how the function terminated, howEnded. Assign the integer 1 to howEnded if the pre-specified tolerance is met, and 2 if the maximum number of terms are used.

3. Test your function in part (b) with four different, well-thought-out input variable sets. All four tests are to be made in the same test m-file.

(9). Provided with the following geometric series:

\[S = a + ar + ar^{2} + ... + ar^{n}\]

write a MATLAB program using the while loop to determine the value of S given the inputs a, r, and n.

The program inputs are:

1. the constant, a. (a\(\neq 0\))

2. the value, r (r \(\geq 0\)), and

3. term constant, n as n+1 is the number of terms, n \(\geq 1\).

The program output is:

1. The numeric value of S.

Test and run your program for the following combination of a = 3, r = 2.1, and n = 8.