Module 7: FUNCTIONS
Learning Objectives
After reading this lesson, you should be able to:
write your own functions in MATLAB,
use the rules for creating and naming functions,
write functions in a program m-file in MATLAB,
write multiple functions in one function m-file.
What is a function?
You already know what a function is because we have been using MATLAB
built-in functions through this whole book! Simply put, a function is a
piece of code with explicit input and output variables. A function
performs a task for you. For example, the function sin() takes a
number in radians as its input and returns the sine of the input. It is
executed whenever/wherever it is called in an m-file. Of course, the
sine of a number is not magically found: there is some code behind the
scenes. In this module, we will show you how to create and use your own
custom functions.
The functions you make are called “user-defined” functions. These are no different conceptually than the “built-in” MATLAB functions you have been using so far in the course. We use “user-defined functions” as a shorthand to indicate it is a custom function that we write ourselves.
The lines of code that are below the function statement (see Example 1b) are called the body of the function, and contain standard MATLAB code. This is where all processes, operations, or logic tests are placed in the function.
What are the naming rules for functions in MATLAB?
Similar to naming m-files and variables, there are rules for what you
can name functions. In fact, they are the same rules as those for
m-files and variables, which you can review in Lesson 2.1. In addition
to those rules, the name of the function must be the same when it is
defined and when it is called. For example, if you defined a function
and name it myFunc(), then you must use the same name when you call it
(myFunc()).
How can I create functions in MATLAB?
User-defined functions exist in many popular programming languages. MATLAB functions, just like in other languages, have input and output variables, which need to be defined both when the function is created and when it is called.
Some general steps to follow when you are creating functions in MATLAB are given here. These steps apply to functions that are saved in a separate m-file as in Examples 1, 2, and 4.
Choose input and output variables for your function. Think about how your function will be used.
Save the function in the same folder as your main m-file.
Write your code in the function.
Make sure all changes in your function m-file are saved so they will be reflected when you call the function.
Define the input and output variables in your main m-file.
Call the function in the main m-file, and test run the main m-file.
When beginning to write a function, one may not know exactly how many outputs or inputs the function will have. To help determine this, it is a good idea to develop a flowchart (Lesson 6.1) or pseudocode (Lesson 6.2) of the process before making the function.
The first method that we cover for creating a MATLAB function is to make two separate m-files: one for defining the function (Example 1b) and one for calling it (Example 1a). We need the m-file given in Example 1a because a function must be called in order to run (execute its code). You cannot run the function file simply by pressing “Run” from inside the function m-file like we have been doing for other m-files.
In this method, the function m-file must have the same name as the
function. For example, the code in Example 1b must be saved in an m-file
named myTriangle.m. Failing to follow this rule will return an error.
We present the m-file where the function is called (e.g., Example 1a) first because this is the way we are used to interacting with functions thus far. Next, the function definition m-file is shown (e.g., Example 1b).
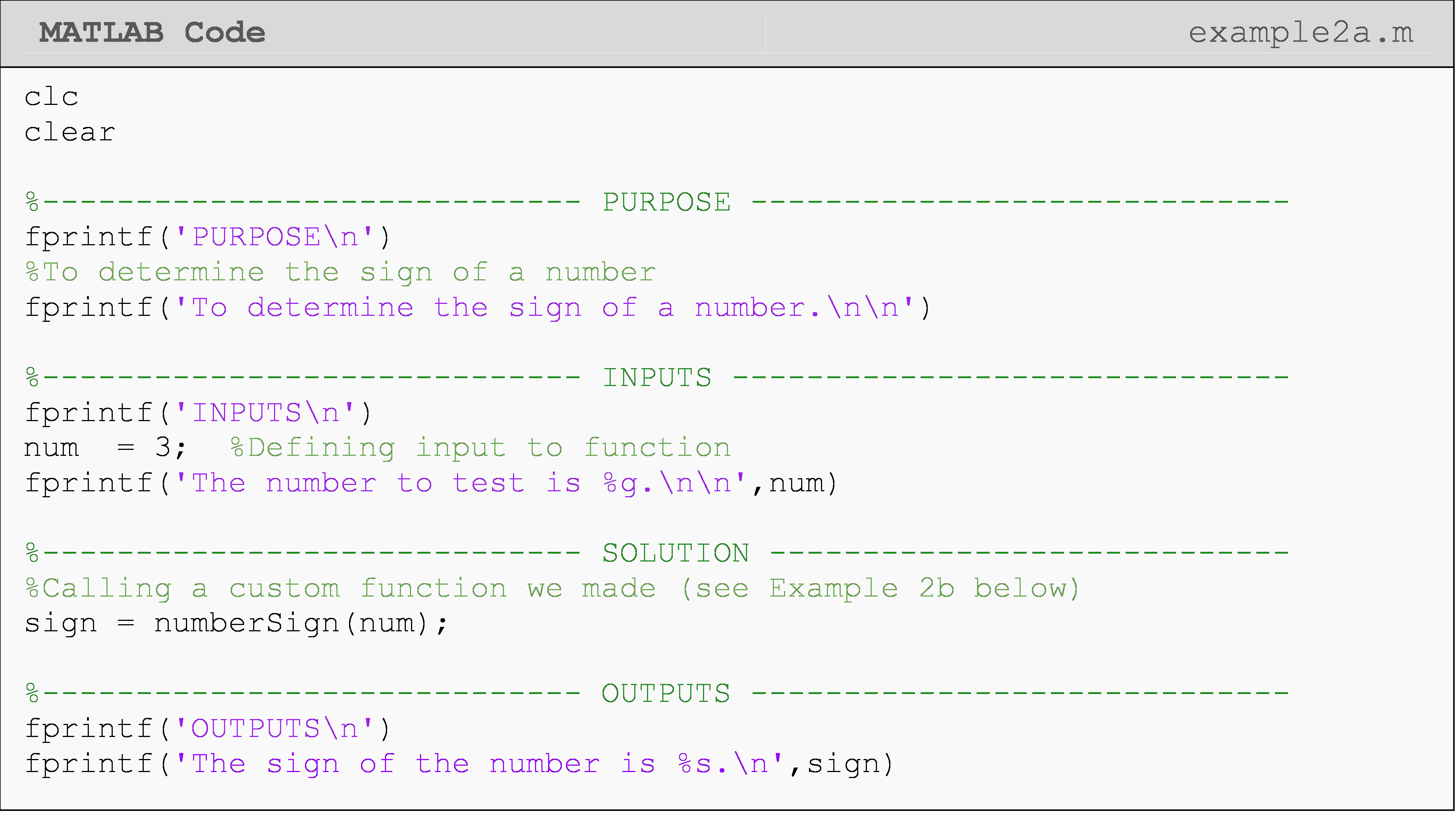
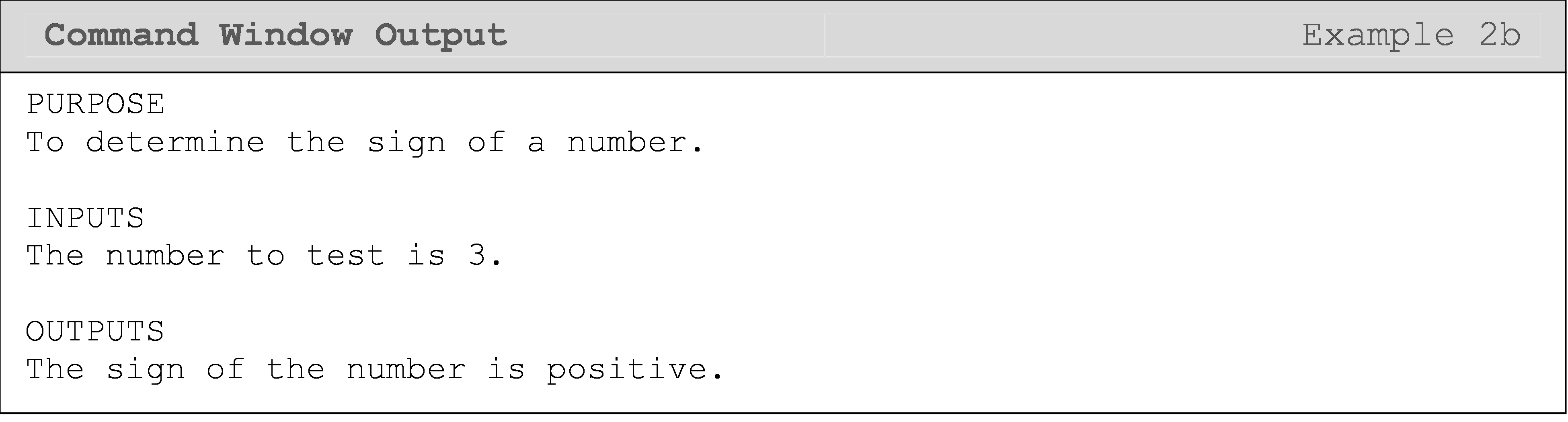
Example 1a
Write and test a MATLAB function called myTriangle(). Given the length
of the three sides of the triangle, it should find the area and
perimeter of a triangle. If a, b, and c are the lengths of the
three sides of the triangle, then the perimeter of the triangle is
\[P = a + b + c\]
and the area of the triangle is
\[A = \sqrt{s(s - a)(s - b)(s - c)}\]
where s is the semi-perimeter of the triangle, and
\(s = \frac{P}{2}\).
Test the program using inputs of a = 3, b = 4, c = 5.
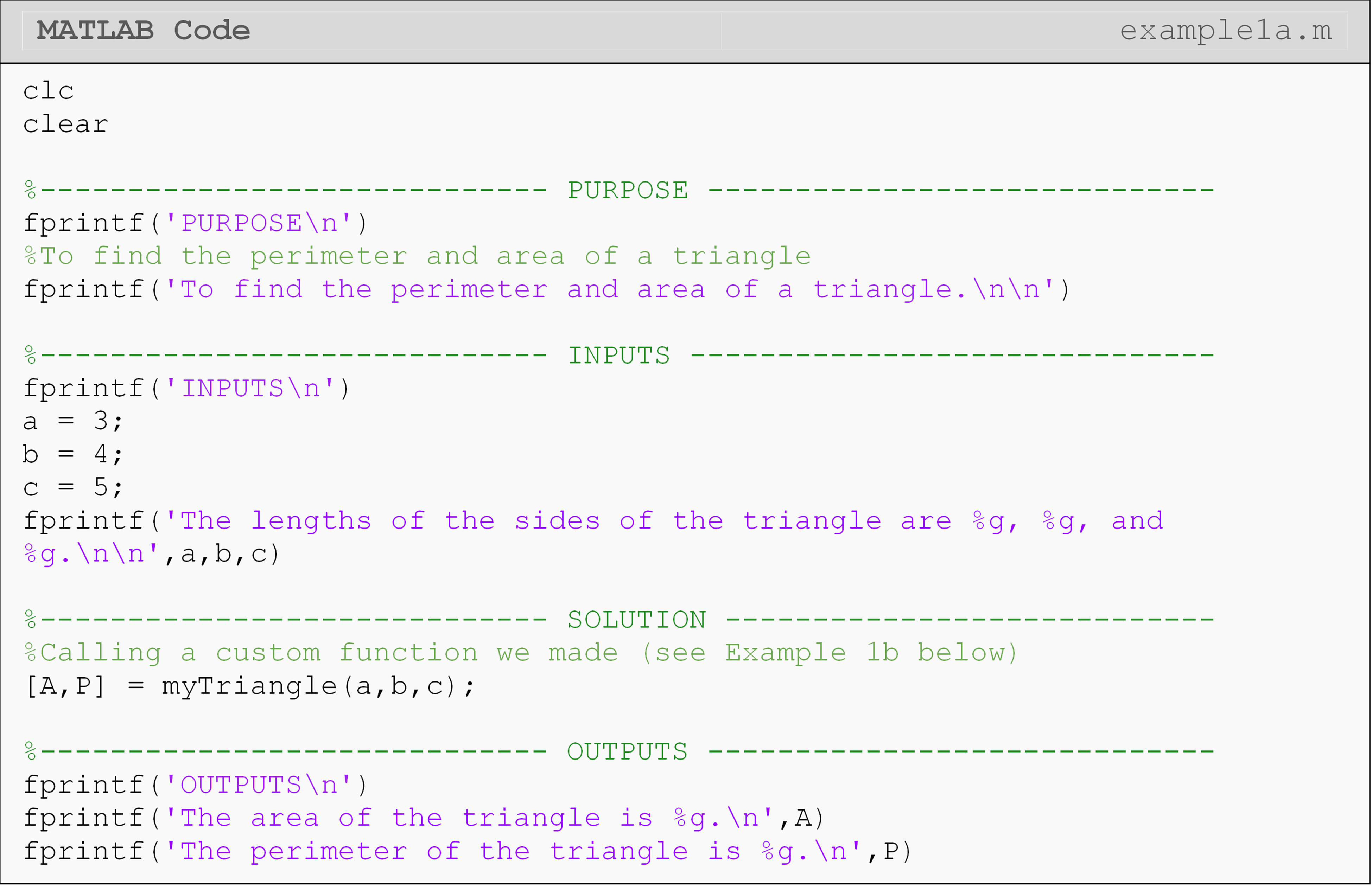
Example 1b
This function is called in the program written in Example 1a. The problem statement is given there.
To write the function, let us first define the desired input and output variables.
Input variables:
a = length a of triangle
b = length b of triangle
c = length c of triangle
Output variables:
area= area of triangleperimeter= perimeter of triangle
The function, mytriangle(), will hence be defined,
function [area,perimeter] = myTriangle(a,b,c)
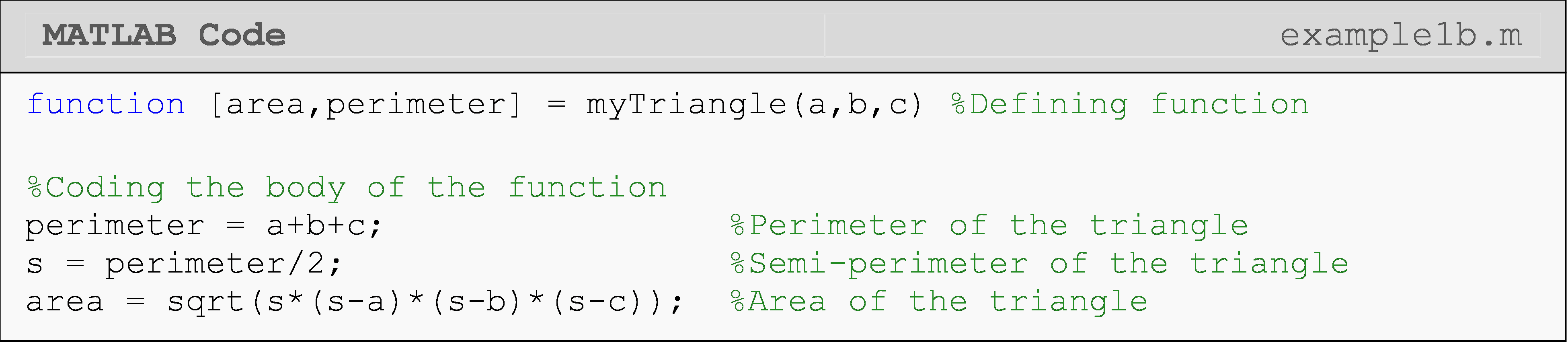

Note that all the statements have been suppressed from showing in the
Command Window in the function myTriangle() (see Example 1b).
Unsuppressed statements can confuse the user of a function, who may be
using it transparently just as one uses the MATLAB functions such as
cos(), int(), etc.
The result from the function myTriangle() is returned to the m-file
where the function is called (see Example 1a), which can then be
displayed to the Command Window if the user chooses to.
To avoid confusion, follow these five rules for developing a function:
always save your function m-file as the function name,
do not assign inputs in the function m-file,
never use
clc,clear, orclosecommands in the function,suppress all statements by placing the ; at the end of each statement,
avoid displaying information (using the
disp()orfprintf()) inside the function m-file.
Although the variables within the function file must be consistent, they
do not have to be the same when you call the function. Think about any
MATLAB function you have called:
sin(), for
example. You have no idea what the variables names are inside the
predefined function
sin(), and you
could use any input or output variable names when you called the
function. That is, both output1 = sin(input1) or sinVec = sin(vec)
or any other combination of valid variable names will work. However,
input and output variable names must be consistent throughout the
function m-file where it is defined (see Example 2b et al.).
MATLAB also needs to know where to find the function m-file when you call it. The easiest way to achieve this is to put both m-files in the same folder, and this is typically what you should do. If you need to access the function file often in different programs, look at the documentation for adding the function directory (folder) to a MATLAB path. This means the m-files will not have to be in the same folder, and MATLAB will automatically “find” them.

Can I define functions in the program m-file?
For the MATLAB version R2016b and later, MATLAB allows us to define
functions in the same m-file as the program we call them in. That is, we
can define and call a function in the same m-file as seen in Example 3
(we do not have to create a separate file). This is the second method
for defining MATLAB functions that we will cover in this lesson. An
end is required for functions that are defined in a program m-file
(see Example 3). It can also be required in other cases (see Example
4b). To be safe, you can default to always putting an end to terminate
your functions.

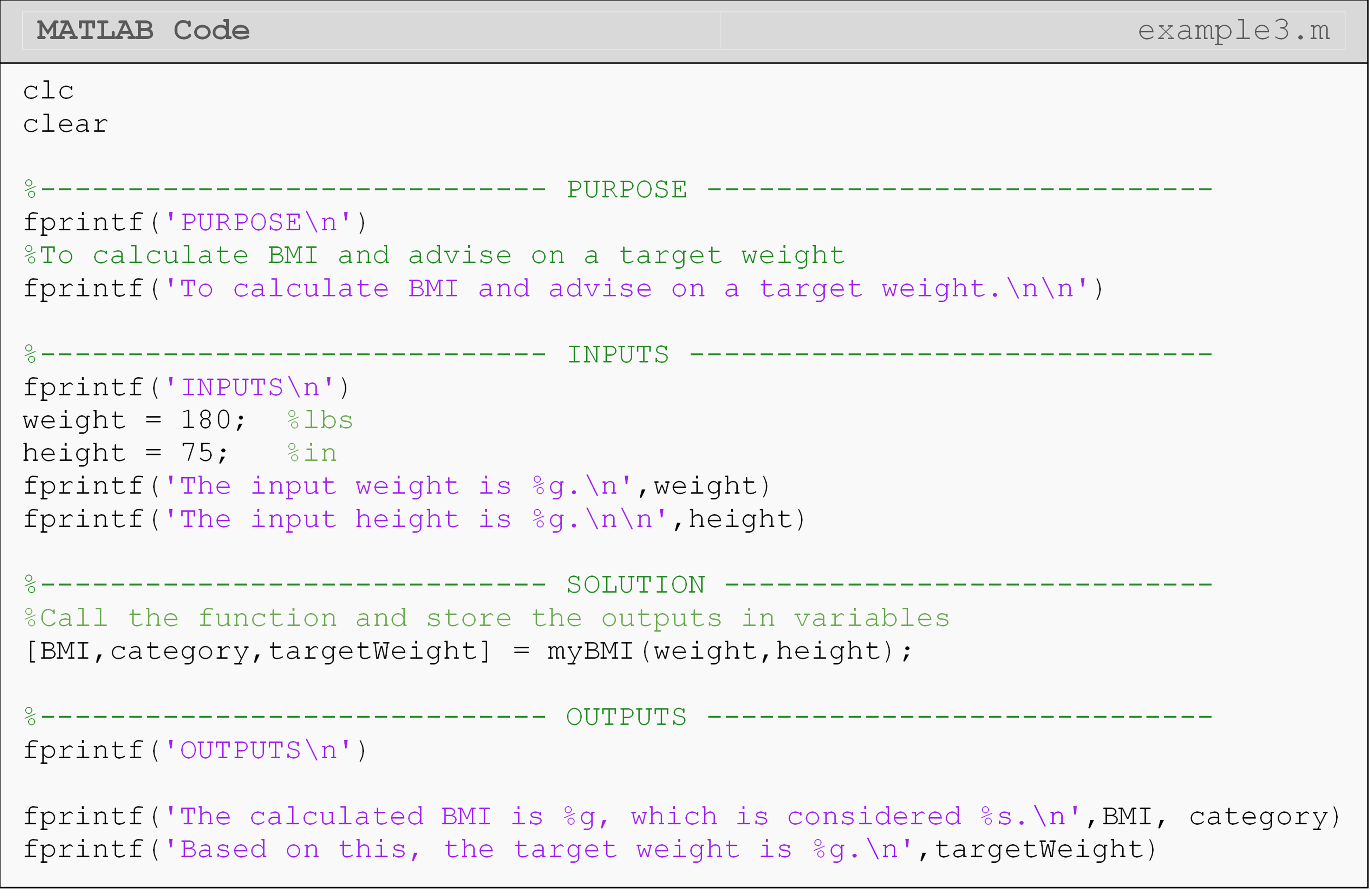
Example 3
In 1998, the federal government developed the body mass index (BMI) to determine healthy weights. Body mass index is calculated as 703 times the weight in pounds divided by the square of the height in inches. The obtained number is then rounded off to the nearest whole number (Hint: 23.5 will be rounded to 24; 23.1 will be rounded to 23; 23.52 will be rounded to 24). The criterion for the weight category is simplified for the example as is given below.
\(BMI < 19\) – Underweight
\(19 \leq BMI \leq 25\) – Healthy Weight
\(BMI > 25\) – Overweight
Write a function that accepts weight (lbs) and height (in) as input
variables, and outputs the BMI as an integer, weight category as a
string (underweight, healthy weight or overweight), and the target
weight (lbs) as an integer. The target weight of an underweight person
would correspond to a BMI of 19, and that of an overweight person to a
BMI of 25. No fprintf() or disp() statements should be in the
function.
function [BMI,category,target_weight] = myBMI(w,h)
Test the program for an individual who weighs 185 lbs and is 75 inches tall.
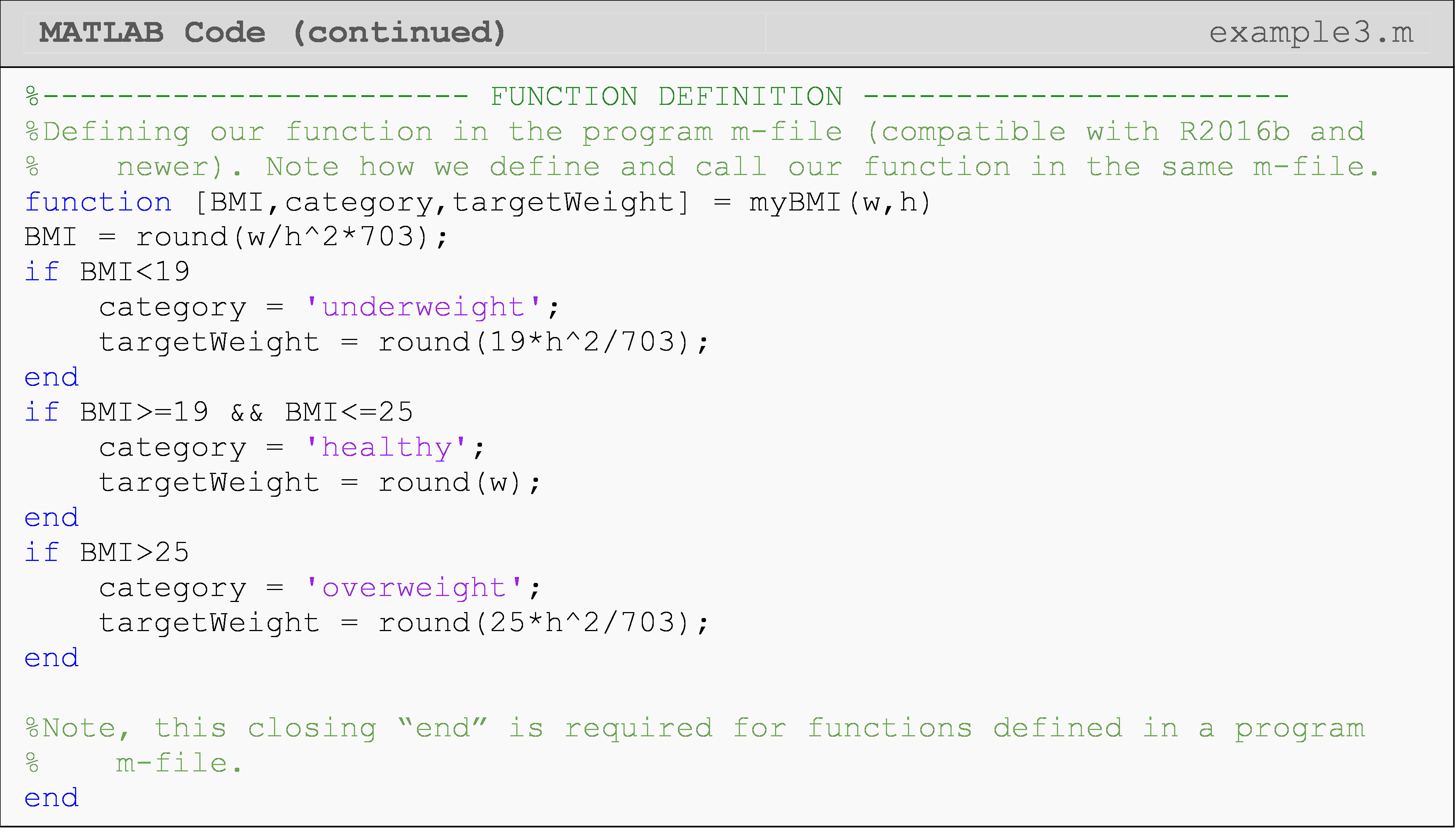

The choice of whether to put the function in a program m-file (define and call in the same m-file) or define the function in its own separate m-file is completely up to you (provided your version of MATLAB supports it). One of the reasons you might choose to define the function in a separate m-file is if your program is already long and/or the function will be used by other programs.
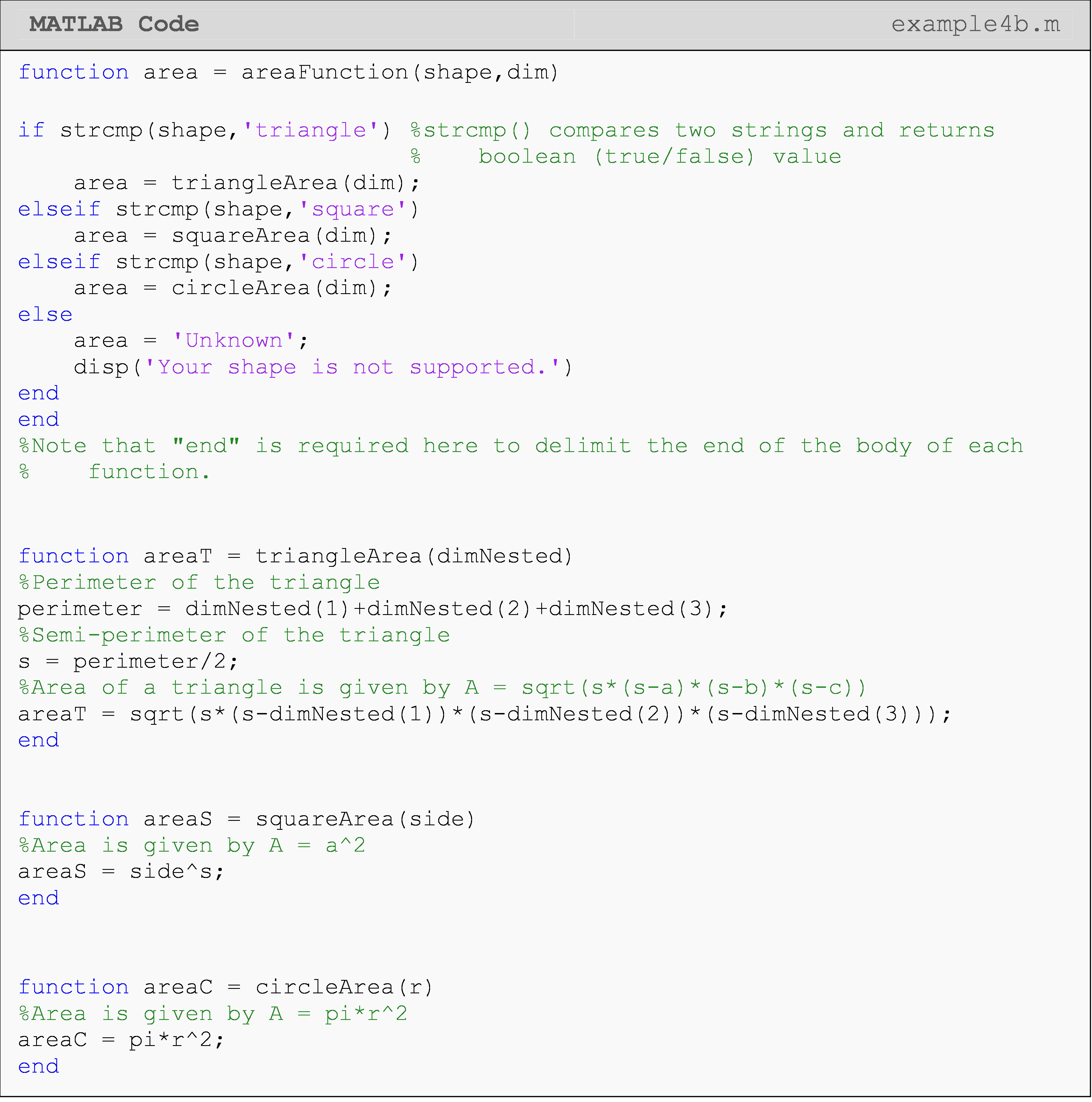
Another function organization option is given in Example 4b where we
define multiple functions in one function m-file: again, only for
convenience. Note that these functions, such as triangleArea(), are
called within the function areaFunction() in the same m-file.
Therefore, calling areaFunction() will call the appropriate area
calculation function, such as triangleArea(), and execute its code.
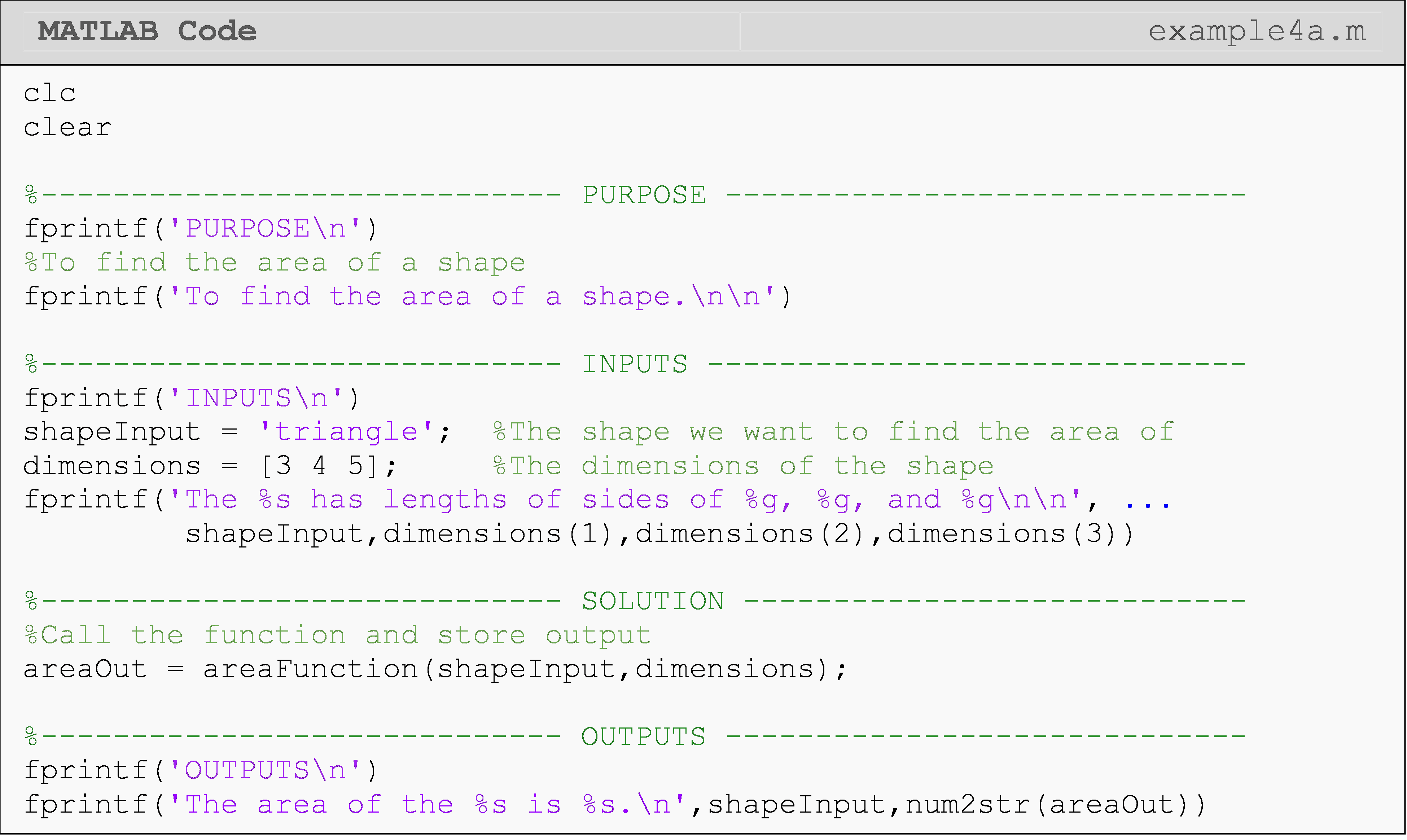
Example 4a
Write a program that calls a function, which finds the area of a given shape. The program should work for three different shapes: triangle, square, and circle. Inputs to the program and the function are a string containing the name of the shape and its dimensions.
Test the program for a triangle with sides of lengths 3, 4, and 5.
Lesson Summary of New Syntax and Programming Tools
| Task | Syntax | Example Usage |
| Create a MATLAB function | function |
function out = name(in);\
out = 4*in; end |
Multiple Choice Quiz
(1). To write a function named myOwnSin(), the function m-file should
be named as
(a) anything I want
(b) myOwnSin.m
(c) myOwnSinfunction.m
(d) sin.m
(2). The following function is written and saved as an m-file called
multmine.m

The function is then called in a separate m-file as follows

The Command Window output is
(a) Undefined function or variable.
(b) 3
(c) 7
(d) 21
(3). What is the cause of the error that is returned when the following
MATLAB code is run? The m-file is saved as example.m.

(a) The required end is not at the end of the inline function
perimeterSq().
(b) The function is not called correctly.
(c) All of the inputs are not defined when the function is called.
(d) All of the above
(4). The following function is written and saved as an m-file called
multmine.m

The function is then called as follows
multmine(3,7)
The Command Window output is
(a) Undefined function or variable.
(b) 3
(c) 7
(d) 21
(5). The following function is written and saved as an m-file called
myCheck.m

The function is then called in a separate m-file as follows

The Command Window output is
(a) Undefined function or variable.
(b) 1
(c) 2
(d) 6
Problem Set
(1). Write a MATLAB function that finds the area of a trapezoid given the
length of the parallel sides and the perpendicular distance between
the parallel sides. Name your function, myTrap(), where the function
has three inputs, side1, side2, and height, and the output is area.
Be sure not to use fprintf() or disp() inside the function m-file,
and suppress all statements within the function. Test your function
with at least two different sets of input values.
(2). A simply supported beam is loaded as shown in Figure A. Under the applied load, the beam will deflect vertically. This vertical deflection of the beam, V, will vary along the length of the beam from x = 0 to L, and is given by
\[V=\displaystyle\left\{\begin{split} &\frac{Pb}{6EIL}\left[(-L^2+b^2)x+x^3\right], 0<x<a\\ &\frac{Pb}{6EIL}\left[(-L^2+b^2)x+x^3-\frac{L}{b}(x-a)^3\right], a<x<L \end{split}\right.\]
where,
x is the distance from the left end,
P is the load,
L is the length of the beam,
a is the location where the load P is applied,
E is the Young’s modulus of the beam material, and
I is the second moment of area.
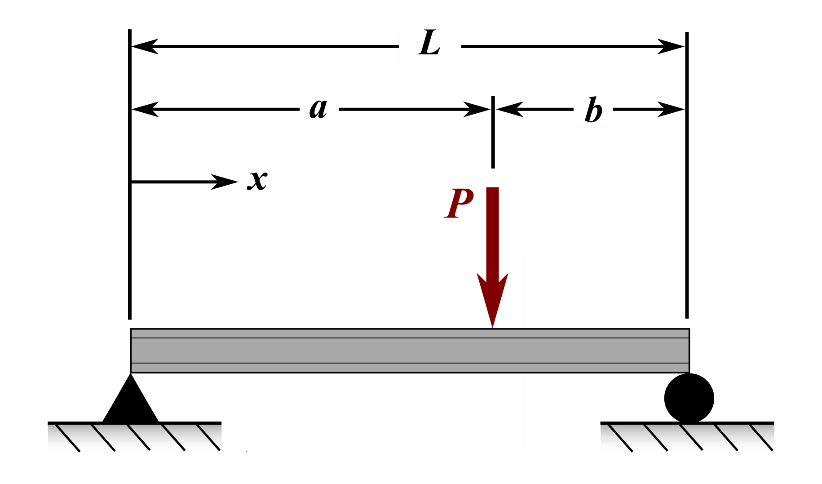
Figure A: Simply supported beam shown with applied load, P.
Complete parts (a) and (b).
Make a flowchart for the problem.
Write a MATLAB function that outputs the vertical deflection of the beam at a point of interest.
The function inputs are
distance from the left end to the point of interest,
x,length of the beam,
L,load,
P,location where the load P is applied,
a,Young’s modulus of the beam material,
E, andsecond moment of area,
I,
and output is,
- the calculated deflection,
V.
In your test m-file, display all of the inputs and outputs by using
fprintf(), complete with explanation and reasonable format.
Run your test m-file for the following two input sets.
\(x = 2.5,\ L = 5,\ a = 3,\ E = 30E6,\ I = 0.0256,\ P = 30\)
\(x = 4.05,\ L = 5,\ a = 3,\ E = 30E6,\ I = 0.0256,\ P = 30\)
(3). The monthly payment on a car loan is given by the formula
\[PMT = \displaystyle\frac{LA*IPM}{1 - (1 + IPM)^{- NM}}\]
where,
PMT = monthly payment in dollars,
LA = loan amount in dollars,
IPM = interest rate in fraction per month (Note the units),
NM = number of monthly payments (Note the units).
Write a MATLAB function myCar() that outputs the monthly payment for
buying a car based on the loan amount (dollars), length of loan
(years) and interest rate (annual percentage rate). The three inputs
to the function are
loan amount entered in dollars,
LA,length of loan entered in integer years,
NY, andinterest rate entered in annual percentage rate (APR),
APR.
The output is,
- the monthly payment on the car.
Test your function at least three times for three different sets of inputs. Your test m-file should show the following in the Command Window.
Loan amount in dollars,
Length of loan in integer years,
The interest rate in annual percentage rate,
Monthly payment in dollars.
(4). The three principal stresses \(\sigma_{1},\sigma_{2},\sigma_{3}\)for the stress state
\[\left\lbrack \sigma_{x},\ \sigma_{y},\ \sigma_{z},\ \tau_{xy},\ \tau_{yz},\ \tau_{zx} \right\rbrack\]
at a point are given by the solution of the nonlinear equation
\[\sigma^{3} - J_{3}\sigma^{2} - J_{2}\sigma - J_{1} = 0\]
where,
\(J_{1} = \sigma_{x}\sigma_{y}\sigma_{z} + 2\tau_{xy}\tau_{yz}\tau_{zx} - \sigma_{x}\tau_{yz}^{2} - \sigma_{y}\tau_{zx}^{2} - \sigma_{z}\tau_{xy}^{2}\)
\(J_{2} = \tau_{xy}^{2} + \tau_{yz}^{2} + \tau_{zx}^{2} - \sigma_{x}\sigma_{y} - \sigma_{y}\sigma_{z} - \sigma_{z}\sigma_{x}\)
\(J_{3} = \sigma_{x} + \sigma_{y} + \sigma_{z}\)
Write a MATLAB function to find the principal stresses, if the stress state is given as a vector of elements. The output principal stresses should be a vector of \(\left\lbrack \sigma_{1},\ \sigma_{2},\ \sigma_{3} \right\rbrack\).
(5). Using your knowledge of conditional statements, write a MATLAB function that evaluates the “hotness” level of water leaving a faucet. Prior to exiting the faucet, cold and hot water are mixed together to adjust the output water temperature, where the hot water level may be adjusted from 0 to 100%. The outlet temperature (\(T_{o}(^{o}F)\)) is rounded to the nearest whole number and may be found by
\[T_{o} = \left( H_{w} \right)165 + \left( 1 - H_{w} \right)62\]
where \(H_{w}\) is the percentage of hot water used and is entered as a
decimal (i.e., 95% is entered as 0.95). There are four “hotness”
levels, which are:
- extremely hot water, \(T_{o} \geq 142^{o}F\)
- hot water, \(110 \leq T_{o} < 142^{o}F\)
- warm water, \(85 \leq T_{o} < 110^{o}F\)\
- room temperature water, \(T_{o} < 85^{o}F\)
Save your function m-file as outletWater.m.
Your function has one input, which is
- the percentage of hot water used (entered as a decimal),
and will have two outputs, which are
a string of characters describing the current water condition, and
the temperature of the water.
Test your function using a hot water input of 84% (entered as 0.84).
(6). United States citizens pay federal income tax, social security tax, and Medicare tax on their wages.
Federal Income Tax: According to the Internal Revenue Service, a single-status U.S. citizen will pay 2018 federal income taxes according to the following chart*.
10% on income between $0 and $9,525
12% on the income between $9,526 and $38,700; plus $952.50
22% on the income between $38,701 and $82,500; plus $4,453.50
24% on the income between $82,501 and $157,500; plus $14,089.50
32% on the income between $157,501 and $200,000; plus $32,089.50
35% on the income between $200,001 and $500,000; plus $45,689.50
37% on the income over $500,001; plus $150,689.50
Social Security tax: In 2018, this is 6.2% on earnings
up to $128,400**
Medicare tax: In 2018, this is 1.45% on all
earnings.** An additional 0.9% applies to individuals who earn over
$200,000.***
Complete the following:
(a). Construct a pseudo code for a MATLAB function to find a person’s total tax dollars owed based on their income. Assume all income is taxable.
(b). Assume all income is taxable and write a function myTaxes() has an
input of the person’s income, income, and then outputs the
federal tax,
fedTax,social security tax,
ssTax,medicare tax,
medTax, andtotal taxes owed,
totalTax.
In your test m-file, display all the inputs and outputs by using
fprintf(), complete with explanation and reasonable format.
Test your function for the following incomes: $32,000, $85,000 and $269,000.
(7). Using your knowledge of conditional statements, write a MATLAB function that determines the letter grade and overall percentage score for a student. The function must use the score breakdown as follows:
Table A: Student grade information.
| Category | Weight | Example Scores |
|---|---|---|
| Homework | 10% | 88 |
| Projects | 12% | 95 |
| Tests | 48% | 76 |
| Final exam | 30% | 91 |
The total score is rounded to the nearest whole number to calculate the letter grade as follows:
\(90 \leq A \leq 100,\)
\(80 \leq B \leq 89,\)
\(70 \leq C \leq 79,\)
\(F \leq 69\)
Save your function m-file as letterGrade.m.
There are three function inputs, which are the
homework score out of 800
test score out of 300
quiz score out of 80
There are two outputs which are
a string containing the student’s letter grade, and
the overall percentage score.
Test your function with the following set of inputs:
Homework score of 620
Test score of 260
Quiz score of 62
References:
* Kelly Phillips Erb, “New: IRS Announces 2018 Tax Rates, Standard
Deductions, Exemption Amounts And More”
<https://www.forbes.com/sites/kellyphillipserb/2018/03/07/new-irs-announces-2018-tax-rates-standard-deductions-exemption-amounts-and-more/#28e98d0d3133>
**U.S. Government, “Update 2019 – Social Security”
<https://www.ssa.gov/pubs/EN-05-10003.pdf>
*** U.S. Government, “Questions and Answers for the Additional
Medicare Tax”
<https://www.irs.gov/businesses/small-businesses-self-employed/questions-and-answers-for-the-additional-medicare-tax>