Module 5: CONDITIONAL STATEMENTS
Learning Objectives
After reading this lesson, you should be able to:
identify different relational operators,
construct logical expressions,
perform data type identification with MATLAB functions,
round up, round down, and round numbers to integers.
What are conditions?
Conditions are simply logical expressions: they are not unique to
programming. You are likely familiar with relational
operators
like \(\mathbf{<}\), \(\mathbf{\leq}\), \(>\), etc. (although the syntax may
be slightly different in MATLAB). This is the basic syntax we use to
create conditions in MATLAB. These conditions are either true or false.
Either 4 < 5 (four is less than five) or it is not. Note the last two
operators seen in Table 1 can also be used with non-numeric values like
text. That is, you cannot ask if one word is quantitatively greater than
another, but you can ask if they are the same word or not. Note the
conditional operator for comparing two values to see if they are equal
(==) is not the same as setting a variable equal to a value
(=).
Table 1: Relational operators in MATLAB and what they mean.
| Logical Query | Relational Operator |
|---|---|
Is A greater than `B? |
A > B |
Is A greater than or equal to B? |
A >= B |
Is A less than B? |
A < B |
Is A less than or equal to B? |
A <= B |
Is A equal to (the same as) B? |
A == B |
Is A not (the same as) B? |
A ~= B |

In Example 1, you can see some examples of these relational operators.
They return logical values (true or false), which we will discuss in
more detail later in this lesson.
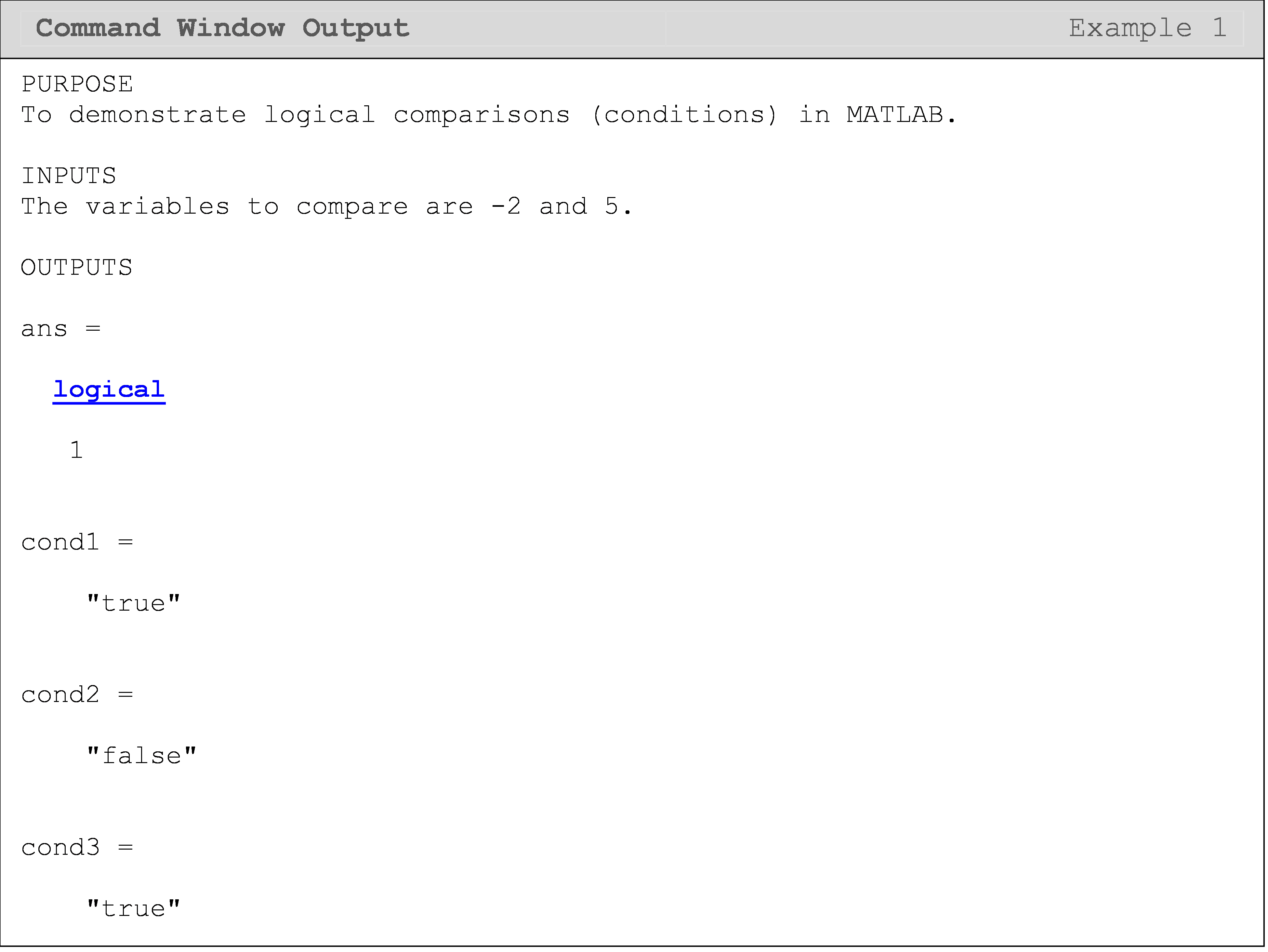
Example 1
Given two variables a and b, conditionally check whether
ais less thanb,ais equal tob, orais not equal tob.
You may assume that a and b each store a value that is a real number.
Solution
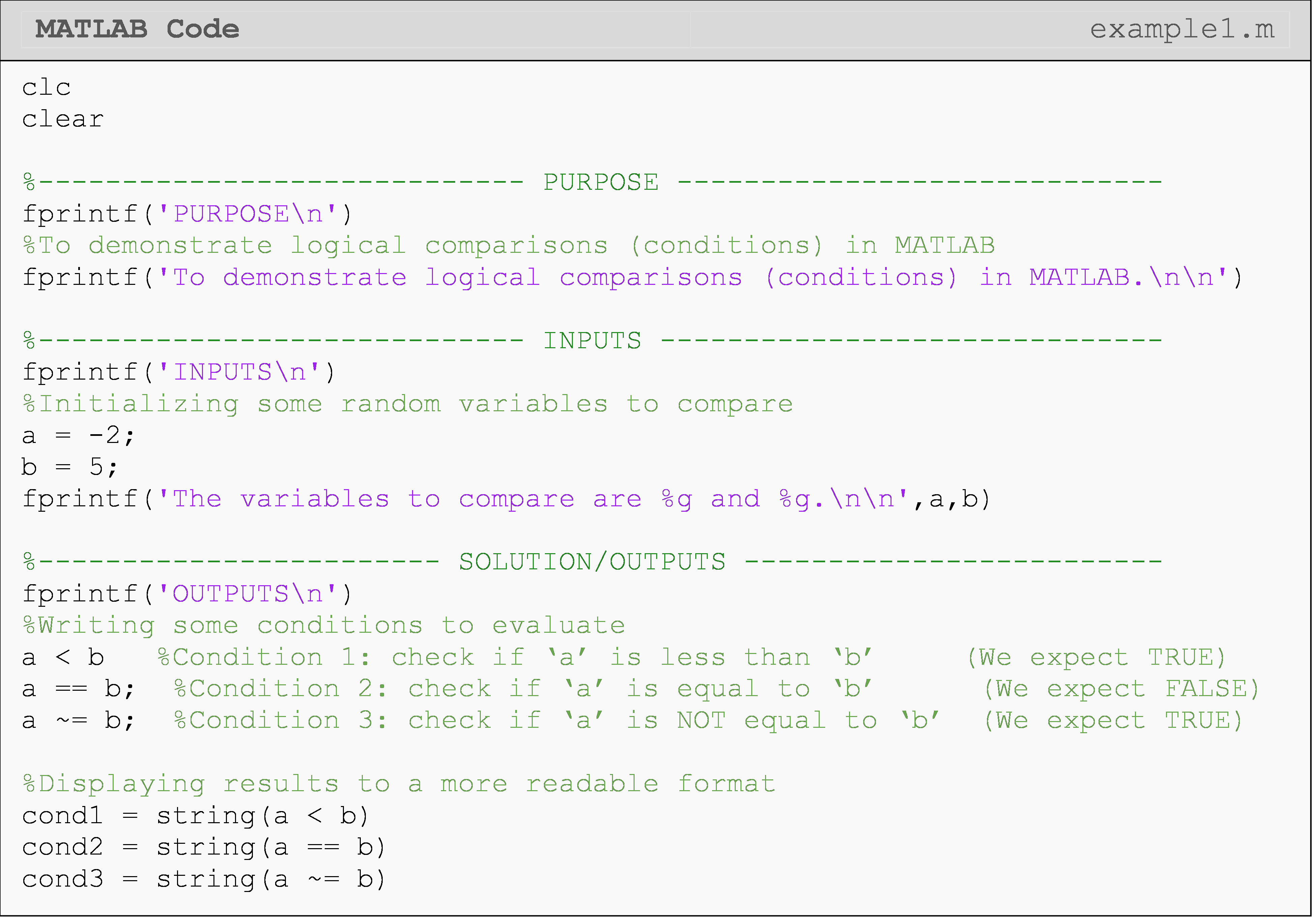
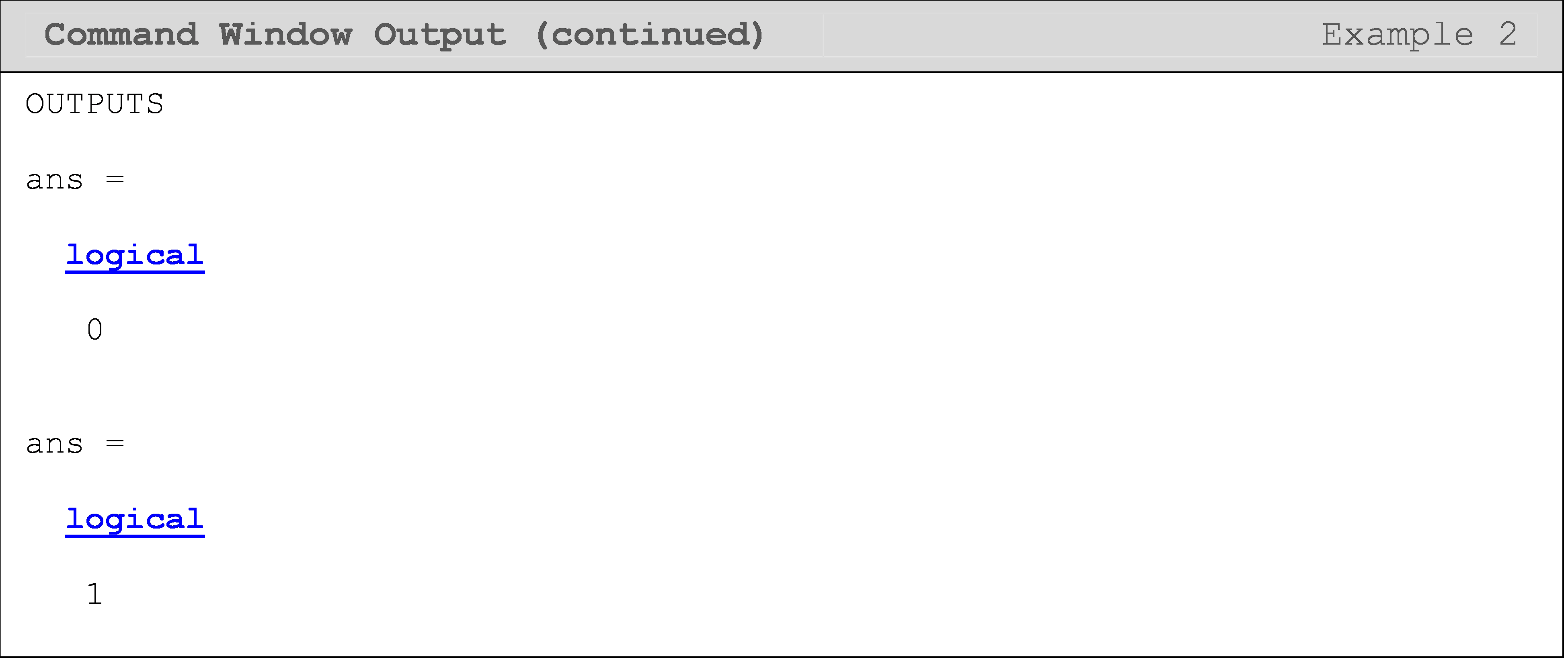
In the last part of the solution, we convert the native output of a
logical comparison into a more readable format using the MATLAB function
string(). Observing the program outputs shown in Command Window reveals
that a logical comparison like a < b has a messy output, which includes
the tag "logical". To convert this output to something more readable we
use string().
What is Boolean logic?
Boolean values of 1 and 0, or
true and
false,
respectively, represent a new data type in MATLAB called the logical
data type. These values are binary (meaning they only have the two
possibilities) and will act as such in all cases.
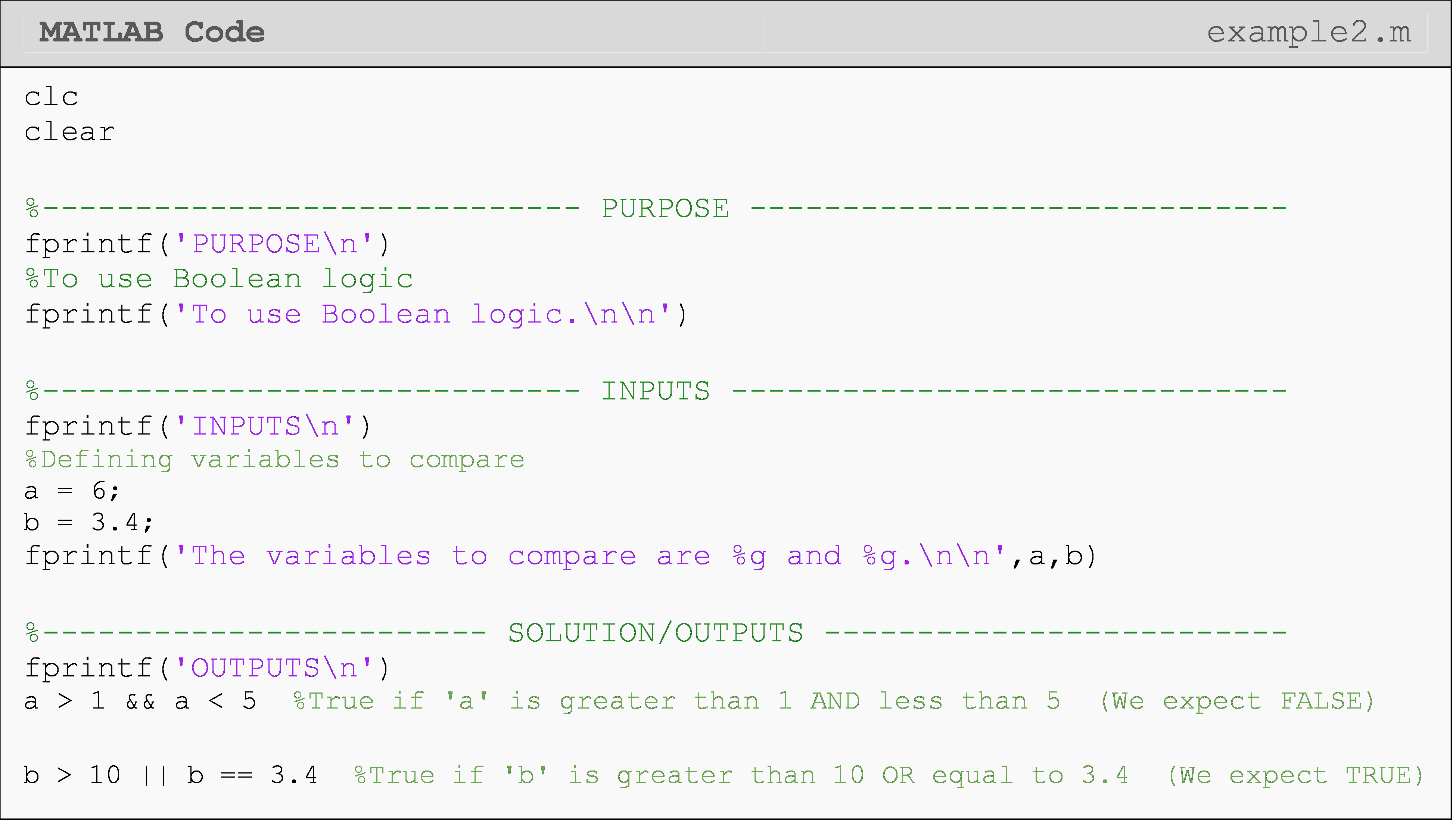
Conditional clauses (expressions that evaluate as true or false like 4 < 5 or 0 == 1) can be stacked together with conditional-linking
operators. That is, we can combine these conditional statements. We will
cover the two most common condition-linking operators:
AND and
OR. Just like we
use the conjunctions “and” and “or” in speech/language to join
independent clauses, we must use them to join two or more conditions
together in conditional expressions. Note that in Example 2 the
conditional-linking operator is
AND (represented
by “&&”) and OR
(represented by “||”).
AND(&&): BothcondA&&condBmust be true for the overall condition to be true.OR(||):EithercondA||condBcan be true for the overall condition to be true.
When using the && comparison, all logic tests joined by the & must be
true for the body of an if-statement to execute. For example, 3>2 && 7>8 would not execute the body of an if-statement.
However, when the || comparison is used, only one of the joined tests
must be true to execute the body. For instance, 3>2 || 7>8 would
execute the body of the if-statement. Finally, (3>2 && 7>8) || 1<=2
would evaluate as true since 1<=2 is true! This is an example of
linking Boolean operators together, which is perfectly valid. As a side
note, you can use
logical()
to convert numeric values to the logical data type in MATLAB. This might
be especially useful when converting a matrix with numerical values to
logical values.
Can different data types be identified in MATLAB?
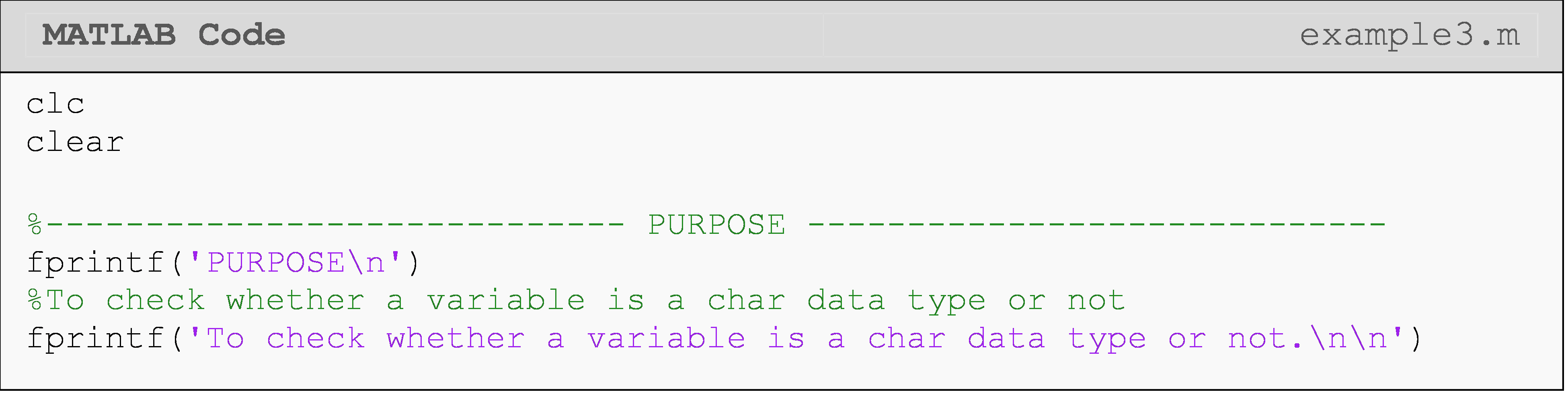
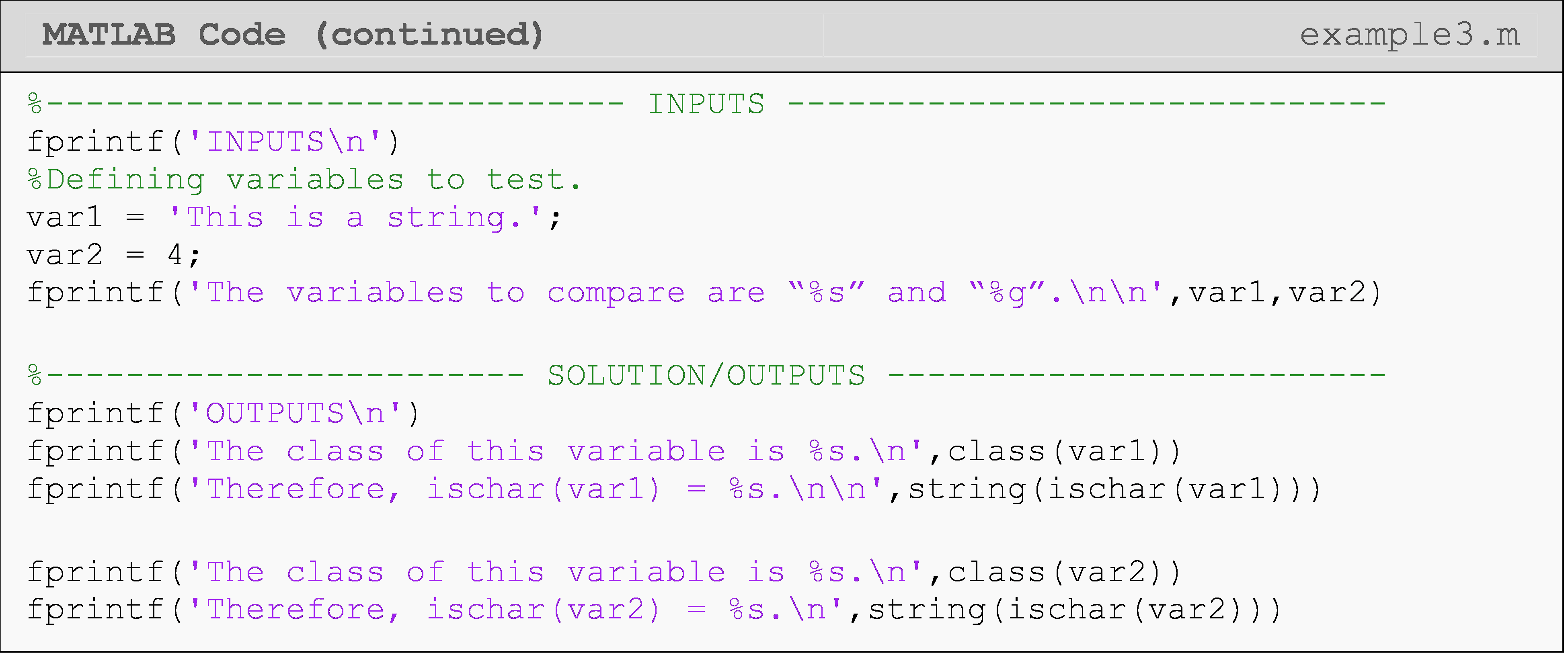
As you have likely experienced by now, data types must be handled with care. As a result, it can be useful to conditionally check the data type of a variable. MATLAB has handy functions for just such a purpose that return a Boolean value, which has a logical data type, of course. (We covered these previously in Lesson 2.5 (Data Types), and include them again here for clarity.)
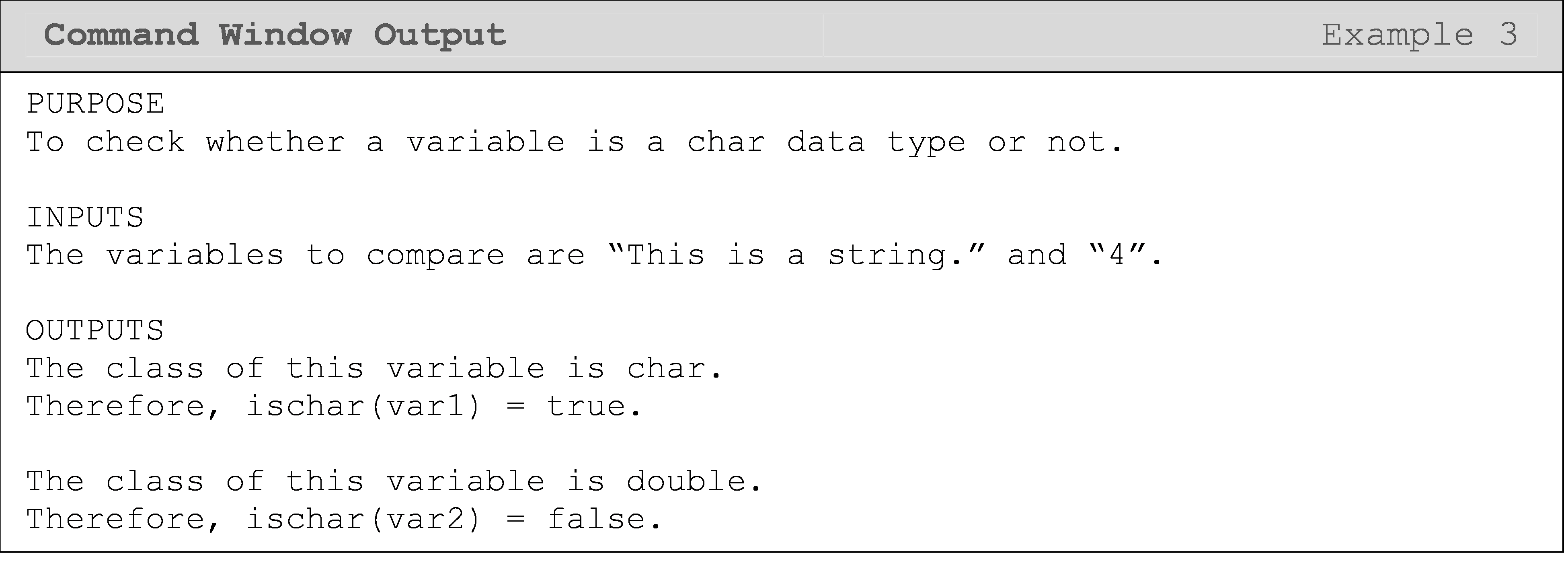
These are called the data type identification functions, and some examples include testing whether a number is real or imaginary with isreal() or whether the value of a variable is a character data type with ischar().
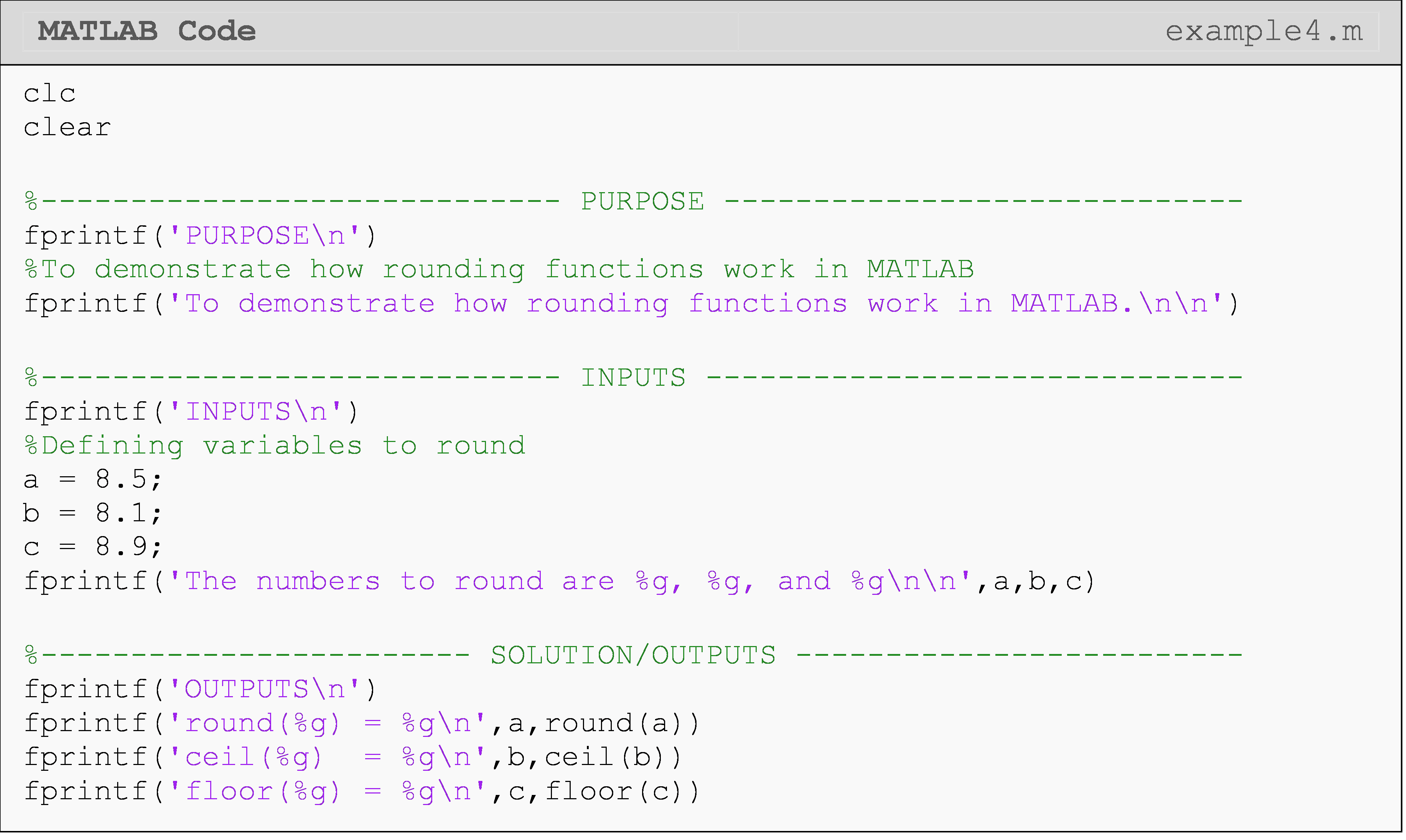
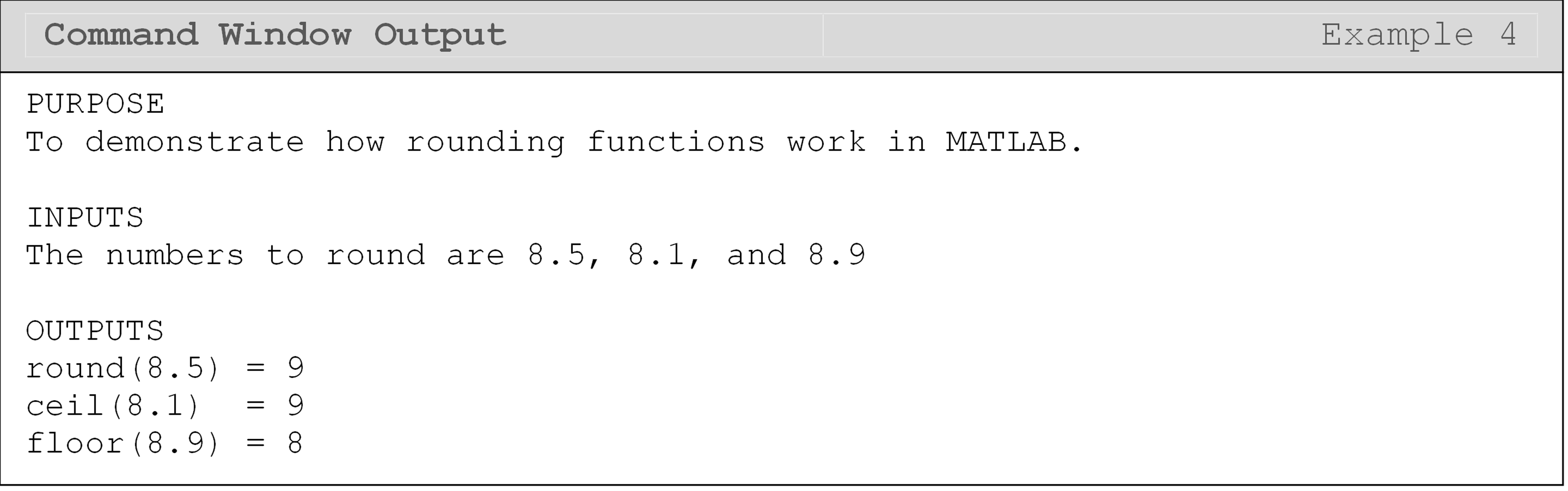
How can I round numbers in MATLAB?
Rounding functions can be very useful in writing effective conditions as we will demonstrate in the following lessons. First, though, we need to know the different rounding functions and how they work. Below is a list of the three most common rounding functions in MATLAB and what they do. You can see each of these functions implemented in MATLAB in Example 4.
round(): returns the nearest integer (“normal” rounding)Example:
round(1.5) = 2Example:
round(1.1) = 1
ceil(): returns the smallest integer that is greater than or equal to the numberExample:
ceil(1.1) = 2Example:
ceil(1.7) = 2
floor(): returns the greatest integer that is less than or equal to the numberExample:
floor(1.3) = 1Example:
floor(1.9) = 1
Lesson Summary of New Syntax and Programming Tools
| Task | Syntax | Example Usage |
|---|---|---|
| Boolean AND operator | && |
a && b |
| Boolean OR operator | || |
a || b |
| Round a number to the nearest integer | round() |
round(a) |
| Round a number up to the nearest integer | ceil() |
ceil(a) |
| Round a number down to the nearest integer | floor() |
floor(a) |
| Check if a variable is a char data type or not | ischar() |
ischar(a) |
| Check if a variable is a real number or not | isreal() |
isreal(a) |
| Determine if A is greater than B | > |
A > B |
| Determine if A is greater than or equal to B | >= |
A >= B |
| Determine if A is less than B? | < |
A < B |
| Determine if A is less than or equal to B | <= |
A <= B |
| Determine if A is equal to (the same as) B | == |
A == B |
| Determine if A is not (the same as) B | ~= |
A ~= B |
Multiple Choice Quiz
(1). The ~= operator stands for
(a) approximately equal to
(b) equal to
(c) greater than or equal to
(d) not equal to
(2). sin(pi)==0 gives false as output because
(a) sin(pi)=1
(b) sin(pi)=-1
(c) sin(pi) is not defined
(d) sin(pi) gives a value other than zero in MATLAB
(3). The operator || stands for
(a) and
(b) or
(c) not
(d) not equal to
(4). The operator && stands for
(a) and
(b) or
(c) not
(d) not equal to
(5). What is the Command Window output of the following program?

(a) a = 60.6
(b) a = 44
(c) a = 60
(d) a = 66
Problem Set
(1). Write a condition that evaluates as true when the given variable
length is greater than 1.5. Test your condition using length = 1 and
then using length = 3.
(2). Write a condition that evaluates as false whenever the given
variable age is less than 21. Test your condition using age = 6 and then
using age = 30.
(3). Write a condition that evaluates as false when base is equal to 5.
Test your condition using a) base = 0.2 and b) base = 5.
(4). Write a set of conditions that evaluates as true when the rounded
value of the given variable num is greater than 16 and less than or
equal to 21. Test your condition using a) num = -8 and b) num = 17.
(5). Write a set of conditions that evaluates as true when the given
variable flag1 is equal to 2 or 3. Test your condition using a) flag1 = 2 and b) flag1 = 0.
(6). An instructor wants to round up students’ grades to the next integer. Write a program that takes students’ grades as an input and returns the integer grades as an output. Hint: you will need to use a vector as the input/output.