Module 5: CONDITIONAL STATEMENTS

Lesson 5.2 – Conditional Statements: if and if-else

Learning Objectives

After reading this lesson, you should be able to:

construct logical expressions,
use if statements to make conditional checks,
use an if-else statement,
make conditional checks if the statement is true or false,
program conditional statements with Boolean logic and multiple expressions.

So far in this text, we have considered only the basic control structure of a sequence. Sequence structure simply implies that statements are executed from the beginning to the end in a sequence. In this lesson, we introduce you to the control structure of conditions. This means that a programmer may want only a certain body of statements executed if a certain condition is true, and some other body of statements to be executed if that condition is false.

What is a conditional statement?

The conditional statement is one of the fundamental programming concepts. The conditional statement runs/executes a block of code if its condition is true. If its condition is false, that block of code will not execute. This is different than the conditional expressions (Boolean logic) we learned in Lesson 5.1. Conditional statements, when true, execute a block of code they contain (see Figure 1), while conditional expressions describe what makes them true (see Example 1).

For example, we might want to display a message that says whether a given number is above 10 (x > 10) or below 10 (x < 10). Obviously, the number cannot be both above and below 10, so we would need to display these messages conditionally.

There are two general types of conditional statements in MATLAB: if and switch statements. We will cover only the if statement since it is the most popular and versatile, but a very similar logic, applies to switch statements if you are curious. The if statement can be extended with the conditional clauses of else and elseif, which we will cover in this and the following lesson (Lesson 5.2).

What is the if statement?

An if statement is the simplest complete conditional statement. It needs only one condition, one line of code in the body, and an “end” to be complete. The logic test or expression is a condition which the if statement checks. The body is code that you want MATLAB to execute if the condition(s) is/are true. The body is defined by the lines of code between the if and end statements in the if-end conditional statement.

Figure 1: Demonstrates the concept behind conditionally executing a block of code.

Once the if-end statement has reached the end, the rest of program will continue from the lines of code below the end of the if-end statement. In its simplest form, the if-end conditional statement has four main components. These are

the statement if
the logic test(s),
the body of the statement, and
the ending statement, end.

In Example 1, we use an if statement with a conditional expression. Here, we use one of the rounding functions we covered in Lesson 5.1 to design a conditional expression that fits our problem. Note that in Example 1 the disp() function will not be executed if the number is not an integer.

Example 1

Given a real number num, write a MATLAB program that displays, “The number is nonnegative”, if the input number is nonnegative (a number is nonnegative if it is zero or positive), or “The number is negative” if the input number is negative. Run and test your program twice, using values of -4.5 and 6.3. Use only if-end statements.

Solution

The program uses two if-end statements, the first checks if the input number is positive, and the second checks if the input number is negative. When writing the program for this example, one must be careful so as not to create a situation where both statements are true. Notice the difference in logic tests between the two statements.

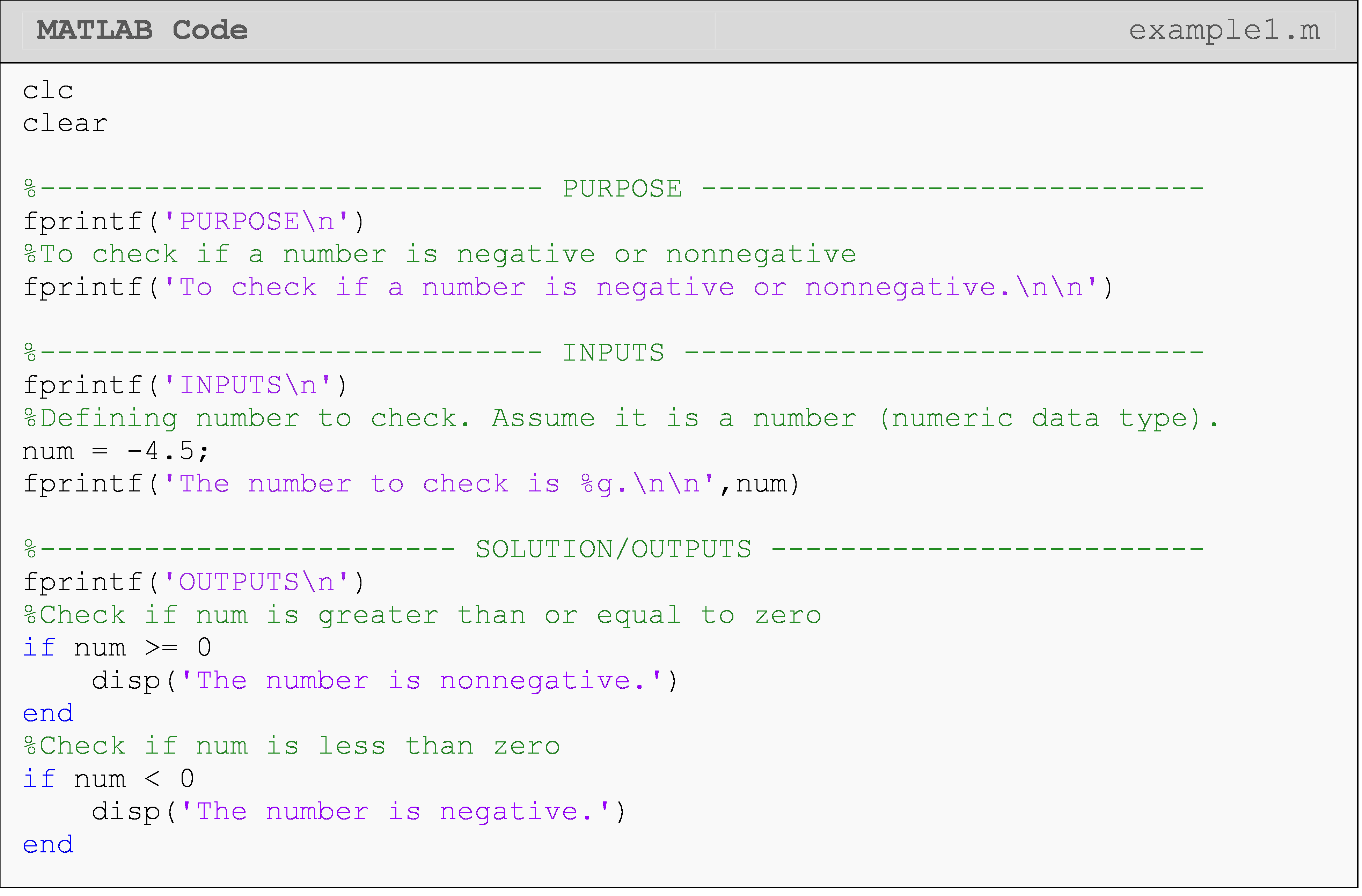
The Command Window output for Example 1 when num = -4.5 is shown next.

The Command Window output for Example 1 when num = 6.3 is shown next.

What is the if-else statement?

The else conditional clause introduces a new component to a conditional statement. Note, else is not a stand-alone component. If used, it must always follow an if statement. Its function is just as it reads: if this condition is true, run this block of code; else, run this other block of code. Therefore, for the else block of code to run, the if condition must be false. This concept can be seen in Figures 2 and 3.

Figure 2: Flowchart of an if-else conditional statement.

Figure 2 shows a more conceptual representation of an if-else conditional statement, while Figure 3 is more of a coding representation (similar to pseudocode). We will go into more detail about flowcharts and pseudocode in Module 6.

Figure 3: Shows how each conditional clause (if and else) each has its own block of code.

Important Notes:

else is not a stand-alone clause: it must always follow if.
For the else block of code to run, the if clause must be false.
There is only one end per conditional statement as seen in Figure 3. One end per if: NOT if-end-else-end.

In Example 2, we add the else or “otherwise” case, which lets us give the user more information in case the if statement is false. For instance, in Example 1, all we could do was to output a message when the if statement was true. Now, we can execute a block of code when the given number is a nonnegative integer and execute another (different) block of code when the number is negative.

Example 2

Solution

Although the output is the same as that of Example 1, this m-file is slightly shorter. This is because MATLAB only needs to conduct one logic test here as opposed to conducting two logic tests in Example 1.

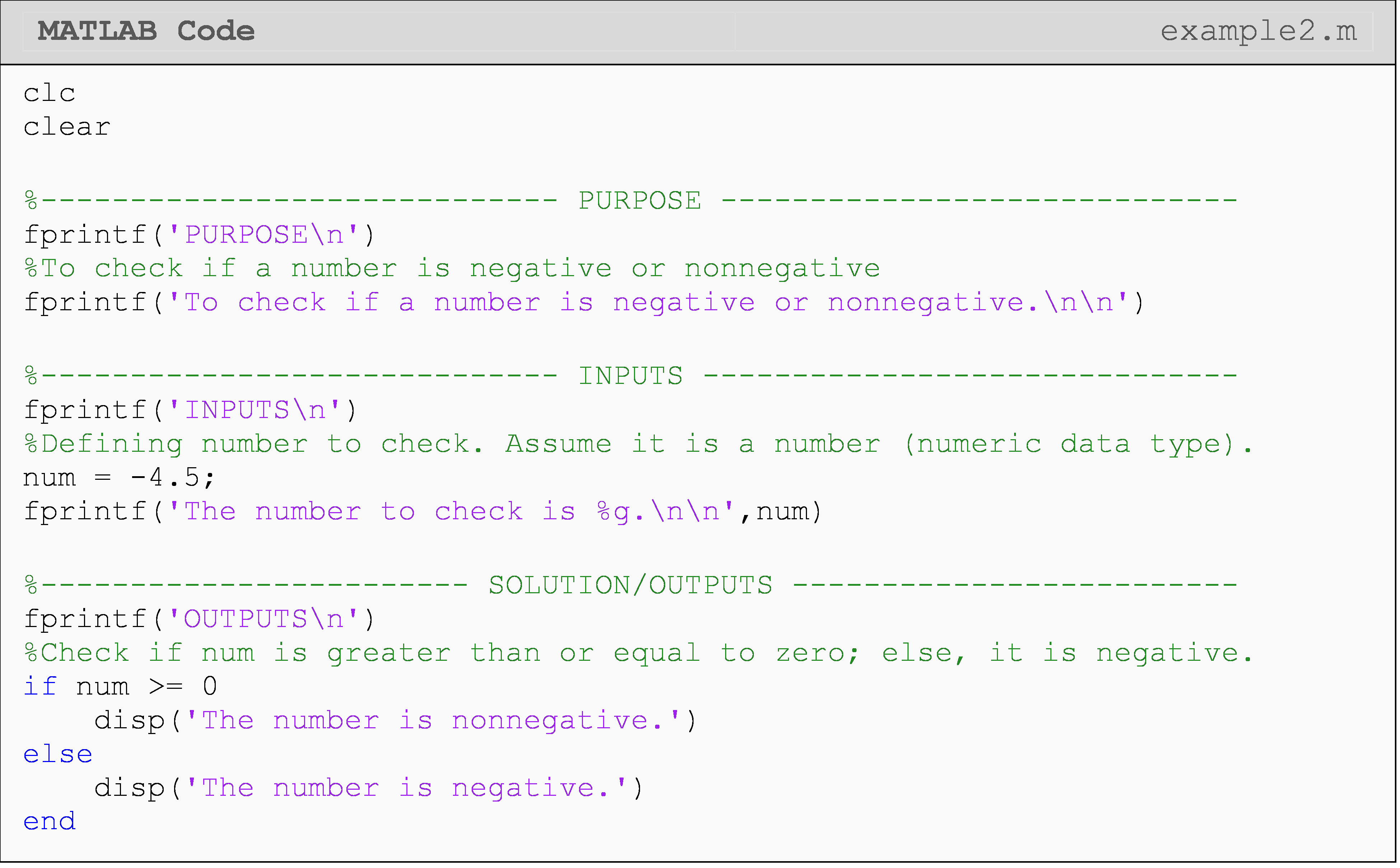
As you can see in Example 2, only the body of the if statement is executed. Once a conditional clause evaluates as true, the block contained is run and then the whole conditional clause is exited. This means else is not considered nor is its code block executed. This is another way of saying the if condition(s) must be false for else to run.

The Command Window output for Example 2 when num = -4.5 is shown next.

The Command Window output for Example 2 when num = 6.3 is shown next.

Important Note: Because a condition cannot be simultaneously true and false, an if-else statement, only the if or the else block runs: never both.

Can I use multiple conditions in a single expression?

We saw how to join two conditional expressions together in Lesson 5.1 with Boolean logic using AND (&&) and OR (||). Now we will look at how to use multiple conditional expressions in a single if statement.

In Example 3, we use multiple conditional expressions in an if statement, which allows us to remove the assumption that the variable holds a number. Try it yourself with a char data type and see what happens!

Example 3

Write a program that checks if a variable is a numeric data type and an integer. Display the result to the Command Window.

Solution

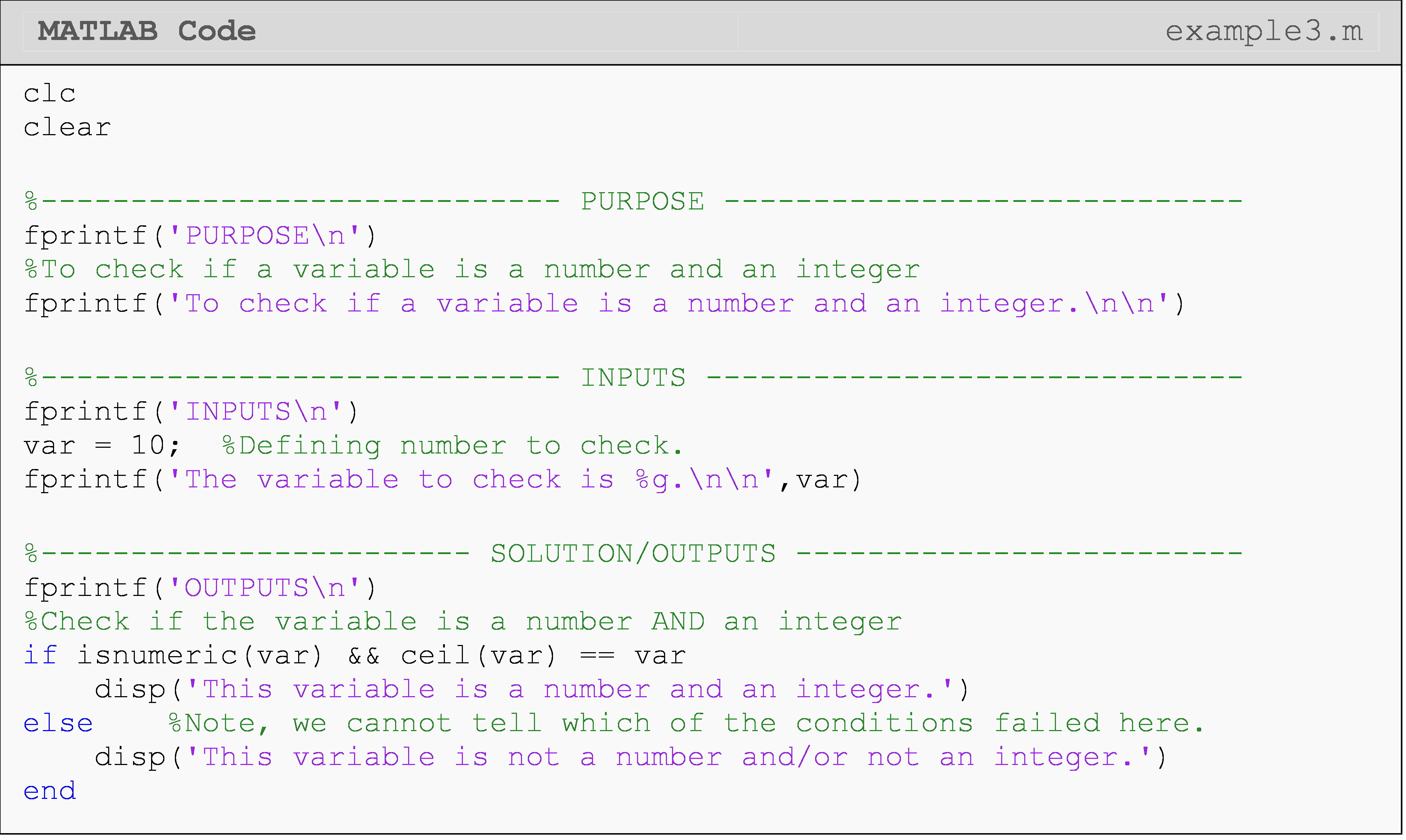
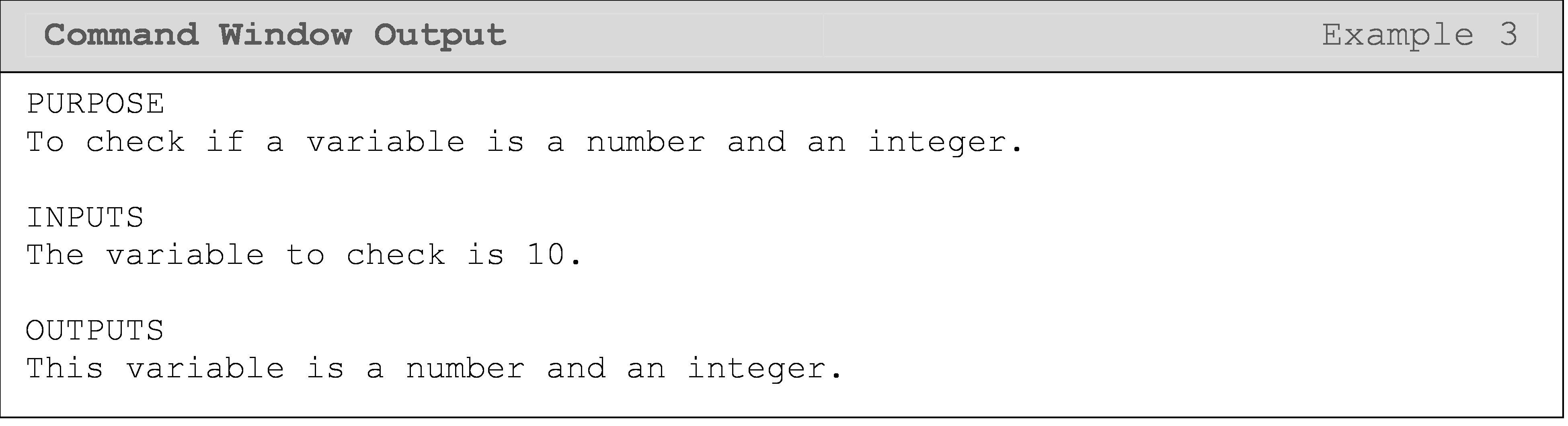
In Example 3, we use two compounded conditional statements joined by an AND (&&) operator. In Example 4, we provide a usage case of the Boolean operator OR (||).

Example 4

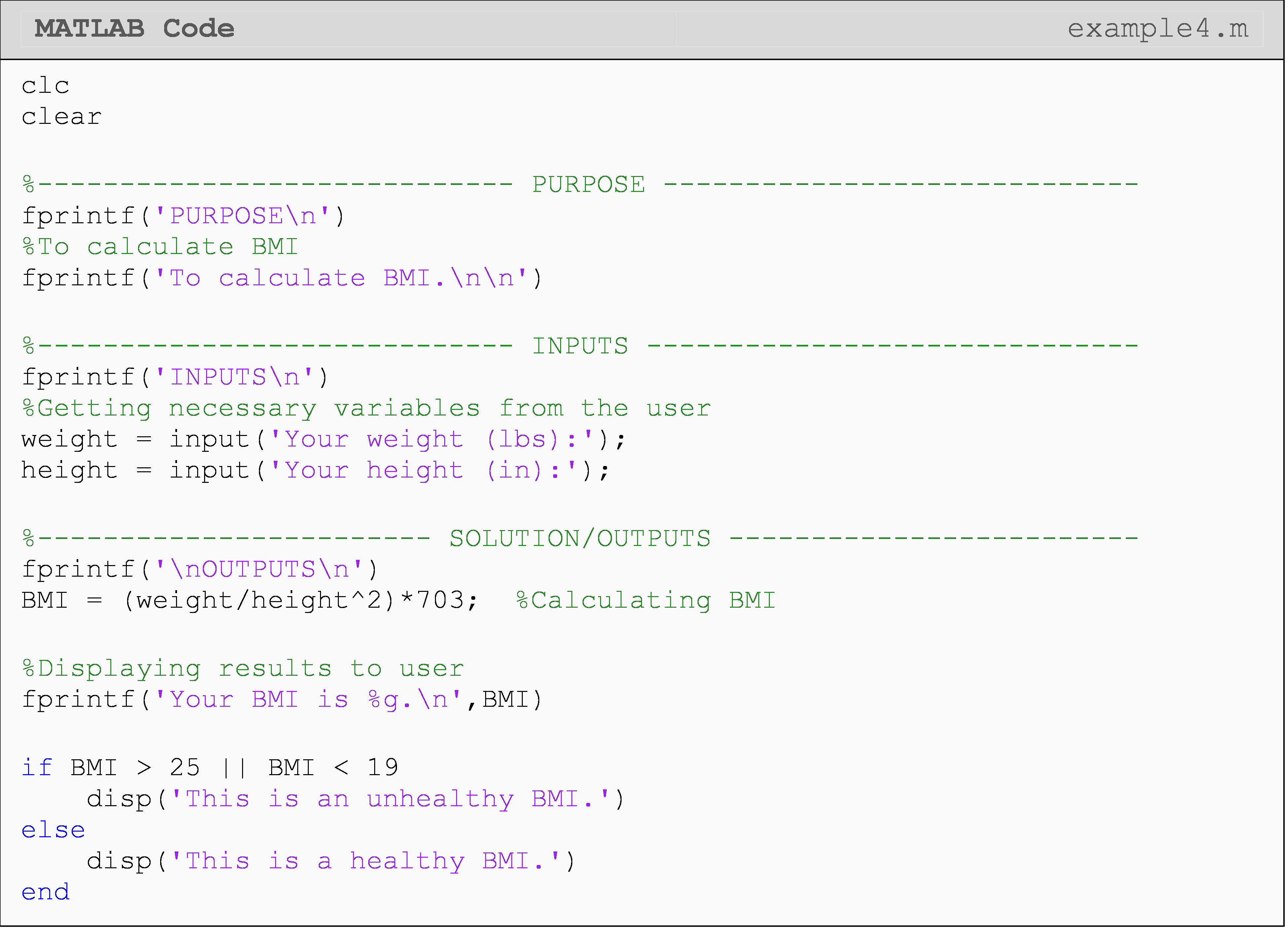
In 1998, the federal government introduced the body mass index (BMI) to determine healthy weights. Body mass index is calculated as 703 times the weight in pounds divided by the square of the height in inches of the individual. The obtained number is then rounded off to the nearest whole number. The criterion for a healthy weight is given as follows.

\(\text{BMI} < 19\) - Unhealthy weight
\(\text{19} \leq BMI \leq 25\) - Healthy weight
\(\text{BMI} > 25\) - Unhealthy weight

Write a MATLAB program that outputs, based on the above criterion, if an individual has a healthy or unhealthy weight. The program inputs are the person’s weight in pounds and height in inches.

Solution

A person’s BMI is calculated by the formula:

\[\text{BMI} = \frac{\text{weight}\text{ }\text{(lbs)}}{\lbrack\text{height}\text{ }\text{(in)}\rbrack^{\text{2}}} \times \text{703}\]

The steps in the algorithm are:

Enter the person’s weight in lbs and height in inches.
Calculate BMI using, \(\displaystyle \text{BMI} = \frac{\text{weight}\text{ }\text{(lbs)}}{\lbrack\text{height}\text{ }\text{(in)}\rbrack^{\text{2}}} \times \text{703}\)
If BMI not in the range of 19 and 25, then the person has an unhealthy weight, else the weight is healthy.

A Note on Writing Good Conditional Statements

As we have previously discussed in Lesson 2.1, mixing double negatives and Boolean values is a bad practice and adds unnecessary complexity in the long run (“ain’t no good”). If you are using variable names inside your conditions, make sure you follow this rule. You can see a detailed explanation in that lesson if you need a review.

Lesson Summary of New Syntax and Programming Tools

Task	Syntax	Example Usage
Conditionally execute a single block of code	`if`	`if 3<5; disp('T');` `end`
Conditionally execute code for both the true and false cases of the condition	`else`	`if 3>5; disp('T');` `else disp('F');` `end`
Use the Boolean AND operator	`&&`	`a && b`
Use the Boolean OR operator	`\|\|`	`a \|\| b`

Multiple Choice Quiz

(1). What is the Command Window output of the following program?

(a) 5

(b) 6

(d) 11

(2). What is the Command Window output of the following program?

(a) 5

(b) 6

(d) 11

(3). What is the Command Window output of the following program?

(a) 1

(b) 2

(d) 79

(4). What is the Command Window output of the following program?

(a) 3

(b) 5

(d) 20

(5). What is the Command Window output of the following program?

(a) 3

(b) 5

(d) 20

Problem Set

(1). Using only conditional statements, write a MATLAB program that determines if any input number, inputNum, is an integer or a decimal number. The program output is “The input number is an integer” or “The input number is a decimal number”.

(2). Using only conditional statements, write a MATLAB program that determines if an integer is even or odd. Display a message to the Command Window telling the user whether the integer is even or odd.

(3). The United States House of Representatives has 435 members. For a bill to pass the house, a simple majority (50% or more) of members have to vote in favor of the bill. Write a program given the variable yes that appropriately outputs either “The bill passed!” or “The bill did not pass!” to the Command Window.

(4). A student’s grade is based on their score in four categories: homework, projects, tests, and final exam. The weight of each category and the student’s scores are given in Table A.

Table A: Student grade information.

Category	Weight	Example Scores
Homework	10%	88
Projects	12%	95
Tests	48%	76
Final exam	30%	91

Write a program that calculates the overall percentage grade of a student. Round up the overall percentage grade to the next integer. Determine if a student has passed or failed the course if the passing grade is 70% or higher.

Use the example case given in Table A to test your solution.

(5). A simply supported beam is loaded as shown in Figure A. Under the applied load, the beam will deflect vertically. This vertical deflection of the beam V will vary along the length of the beam from x = 0 to L and is given by

\[V=\displaystyle\left\{\begin{split} &\frac{Pb}{6EIL}\left[(-L^2+b^2)x+x^3\right], 0<x<a\\ &\frac{Pb}{6EIL}\left[(-L^2+b^2)x+x^3-\frac{L}{b}(x-a)^3\right], a<x<L \end{split}\right.\]

where,

x is the distance from the left end,
P is the load,
L is the length of the beam,
a is the location where the load P is applied,
E is Young’s modulus of the beam material, and
I is the second moment of area.

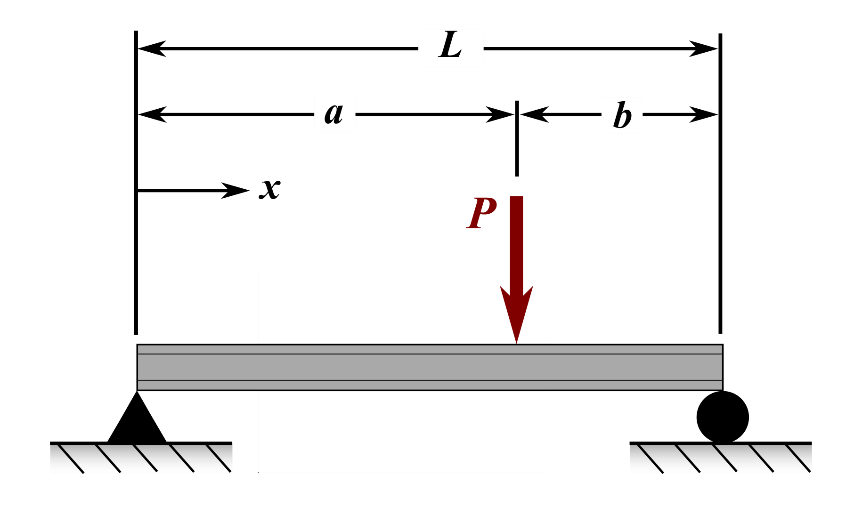
Figure A: Simply supported beam shown with applied load, P.

Write a MATLAB program that outputs the vertical deflection of the beam at a point of interest. Display all of the inputs and outputs by using the fprintf() function complete with explanation and reasonable format.

The program inputs, as entered by input() functions, are

distance from the left end to the point of interest, x,
length of the beam, L,
load, P,
the location where the load P is applied, a,
Young’s modulus of the beam material, E, and
the second moment of area, I,

and output is

the calculated deflection, V

Run your program for the following two input sets. You will need to run the m-file twice: once for each of the two input sets.

\(x = 2.50,\ \ L = 5,\ \ a = 3,\ \ E = 30 \times 10^6,\ \ I = 0.0256,\ \ P = 30\)
\(x = 4.05,\ \ L = 5,\ \ a = 3,\ \ E = 30 \times 10^6,\ \ I = 0.0256,\ \ P = 30\)