Module 8: Loops
Learning Objectives
After reading this lesson, you should be able to:
write programs using for (definite) loops,
use a for loop to plot multiple functions,
decide when to use a for loop vs a while loop.
What is a for loop?
In this lesson, the discussion is limited to the counter-controlled
repetition: that is, the for loop. A
for loop has the
same basic purpose as a
while loop: to
loop, or iterate, over a block of code called the body; that is, to
execute the same lines of code over and over until stopped. The
for loops are
defined by defining a loop counter variable, or “iterator”. The loop
counter variable, or “iterator”, keeps track of which repetition the
loop is on.
The loop counter variable takes the initial value of
startingValue,The loop counter is checked if it is less than or equal to the
endValue(the check is greater than or equal to theendValueif the increment is a negative number).If so, the loop executes the body of the loop, and the loop counter variable is incremented by the value of increment. Step 2 is repeated, and if the check turns out to be false, the loop is terminated.
As we learned in Lesson 8.1 about
while loops,
this is a variable that changes the value after running each loop
iteration. The iterator must have definite bounds (a starting and ending
value), and the
for loop will
stop once it reaches the end of this specified bound. In general, this
means the for
loop will execute the same number of times regardless of all other
conditions.
For example, in the loop definition for i = 3:2:9, the loop counter
variable is named i. It will take the initial value of 3 and end at
9 in increments of 2 (four repetitions will be made with values of
i = 3,5,7,9).
If required, the startingValue, increment, and/or endValue can be
negative.
For example, in the loop definition for i = 11:-3:2, the loop counter
variable is named i. It will take the initial value of 11 and end at
2 in increments of -3 (four repetitions will be made with values of
i = 11,8,5,2).
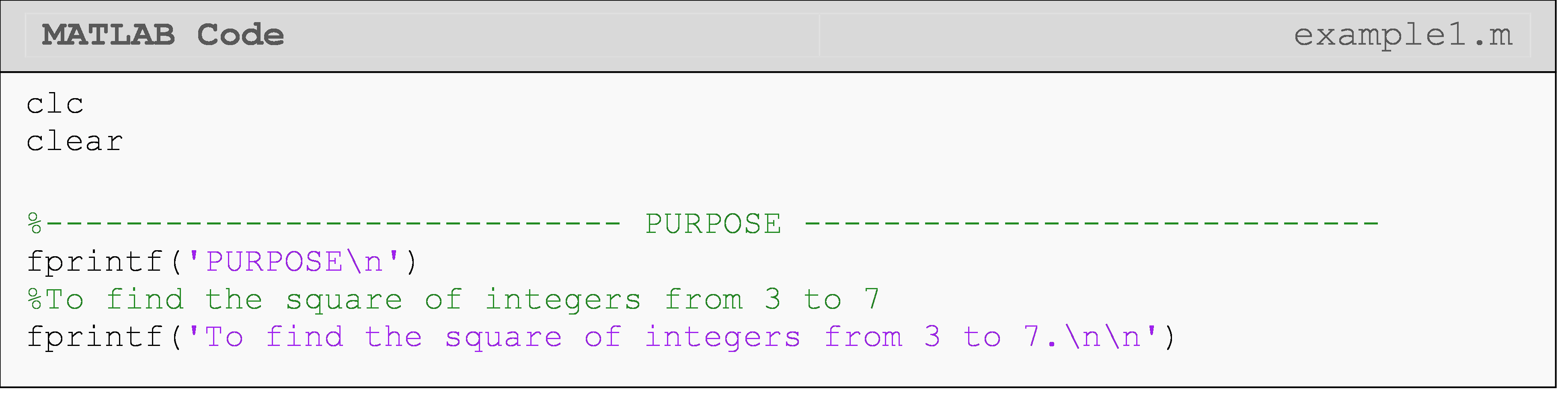
Example 1
Output the square of all the integers from 3 to 7 in the Command
Window.
Solution
If one wants to write out the square of the integers from 3 to 7,
one can write a MATLAB code for it as follows:
\(\;\;\;\;\;\;\;\;\;\) i = 3;
\(\;\;\;\;\;\;\;\;\;\) fprintf('Square of %g is %g',i,i^2)
\(\;\;\;\;\;\;\;\;\;\) i = 4;
\(\;\;\;\;\;\;\;\;\;\) fprintf('Square of %g is %g',i,i^2)
\(\;\;\;\;\;\;\;\;\;\) i = 5;
\(\;\;\;\;\;\;\;\;\;\) fprintf('Square of %g is %g',i,i^2)
\(\;\;\;\;\;\;\;\;\;\) i = 6;
\(\;\;\;\;\;\;\;\;\;\) fprintf('Square of %g is %g',i,i^2)
\(\;\;\;\;\;\;\;\;\;\) i = 7;
\(\;\;\;\;\;\;\;\;\;\) fprintf('Square of %g is %g',i,i^2)
Recall from Lesson 8.1, that this is precisely the type of problem that loops are meant for. In this lesson, we will solve the problem using a for loop. Notice that a pseudocode is first made to help identify what variables are changing and what expressions to display.
Pseudocode for Example 1:
\(\;\;\;\;\;\;\;\;\;\) 1. Start program, clear window/variables.
\(\;\;\;\;\;\;\;\;\;\) 2. Set up a loop to find the square of numbers [Note this can be a for or while loop. Compare with Example 1 of Lesson 8.1.]
\(\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\) Starting number = 3
\(\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\) Final number = 7
\(\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\) Increment by 1
\(\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\) Square each number.
\(\;\;\;\;\;\;\;\;\;\) 3. Display output
\(\;\;\;\;\;\;\;\;\;\) 4. End loop
\(\;\;\;\;\;\;\;\;\;\) 5. End program
Remember, all loops must be terminated with an end statement.
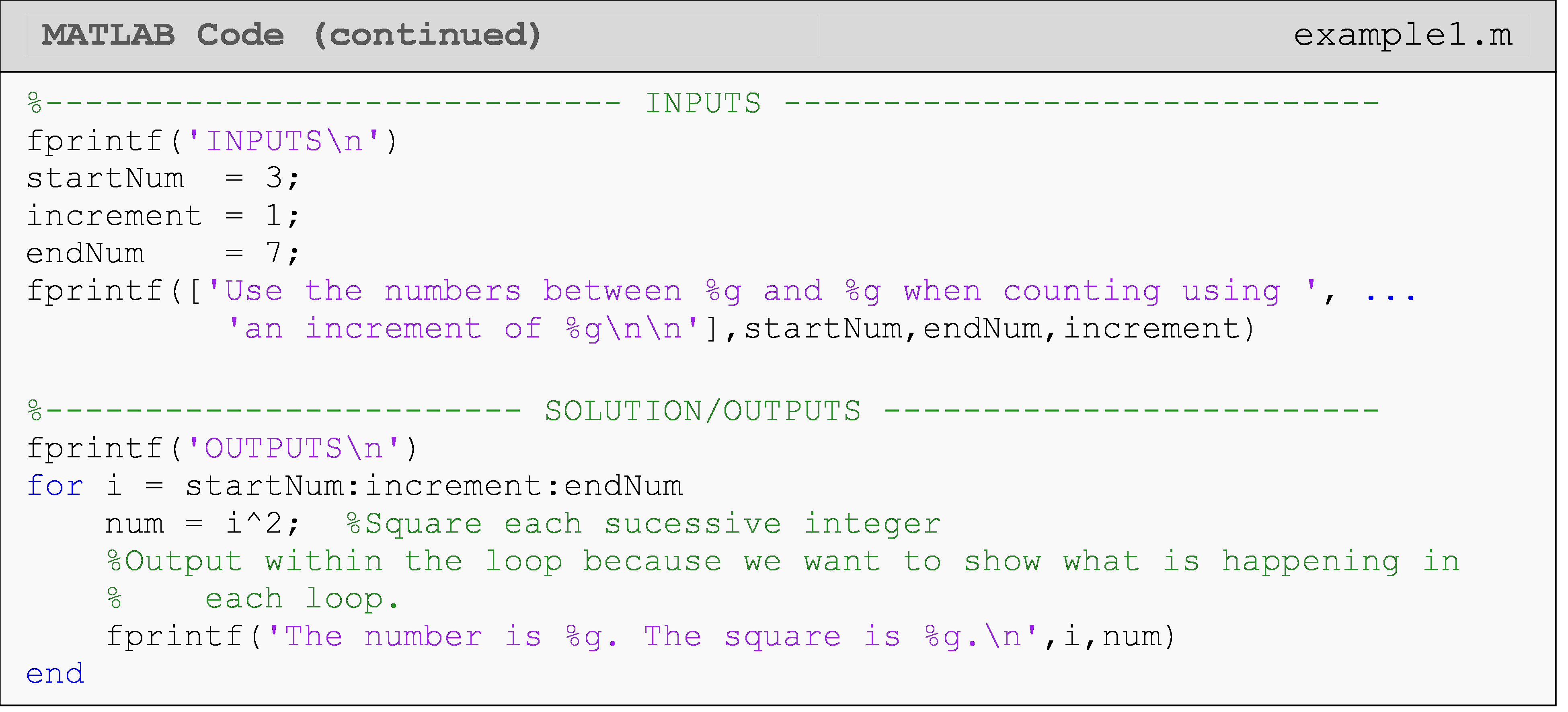
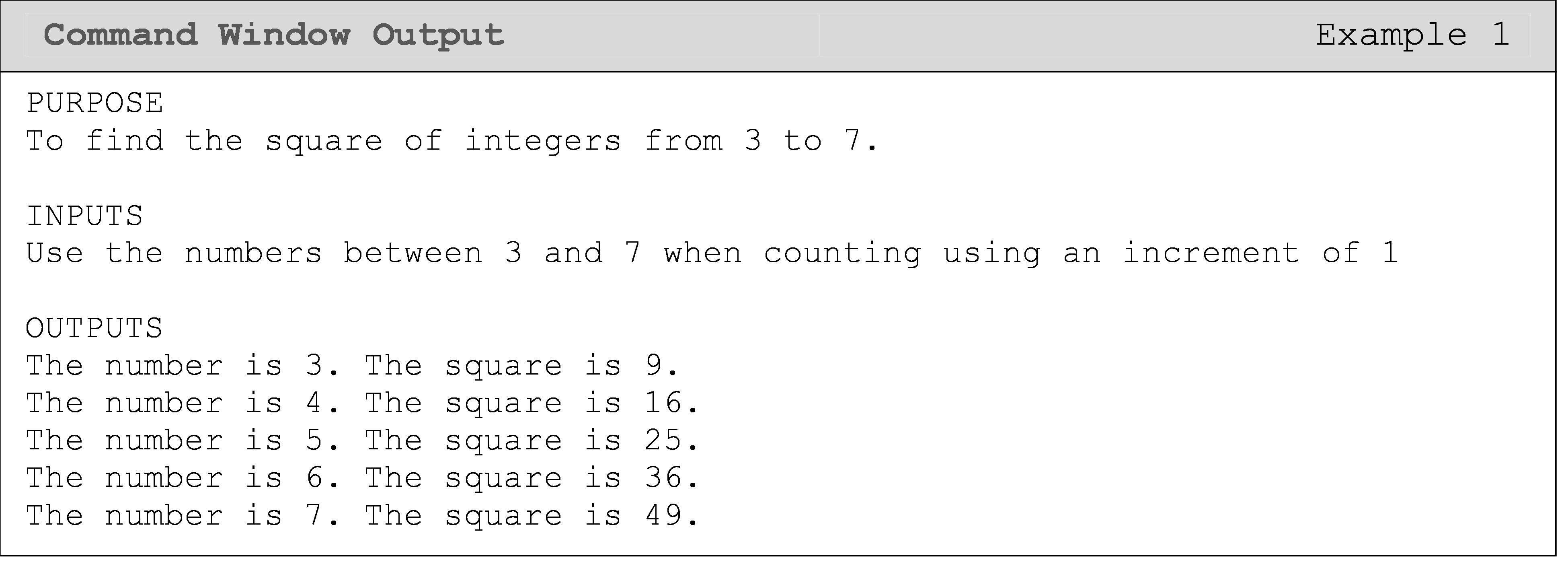
In Example 1, the value of i is changing. The for loop starts with
the value of i being 3, and then increments the value of i by 1
until the loop completes with the value of i being 7. It is
important to understand that the value of the variable i changes and
is checked with each loop repetition.
Take a look at some other examples of how the for loop works.
\(\;\;\;\;\;\;\;\;\;\) for i = 3:1:7
\(\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\) fprintf('Square of %g is %g',i,i^2)
\(\;\;\;\;\;\;\;\;\;\) end
The above for loop would print values of the square of 3, 4, 5, 6, 7 as the loop starts with the value of 3, increments by 1 and stops at 7.
\(\;\;\;\;\;\;\;\;\;\) for i = 3:2:7
\(\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\) fprintf('Square of %g is %g',i,i^2)
\(\;\;\;\;\;\;\;\;\;\) end
The above for loop would print values of the square of 3, 5, 7 as the loop starts with the value of 3, increments by 2 and stops at 7.
\(\;\;\;\;\;\;\;\;\;\)for i = 3:2:10
\(\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\) fprintf('Square of %g is %g',i,i^2)
\(\;\;\;\;\;\;\;\;\;\)end
The above for loop would print values of the square of 3, 5, 7, 9 as
the loop starts with the value of 3, increments by 2 and stops at
9. Although the end limit is 10, it does not get to that value as
the next variable value after 9 would be 11, which is outside the
range.
\(\;\;\;\;\;\;\;\;\;\) for i = 10:-2:4
\(\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\) fprintf('Square of %g is %g',i,i^2)
\(\;\;\;\;\;\;\;\;\;\) end
The above for loop would print values of the square of 10, 8, 6, 4.
The expression used here contains a negative increment, hence the order
of the outputs.
### Example 2 {-}
Output in the Command Window the square of every other integer from 1 to 8.
Solution
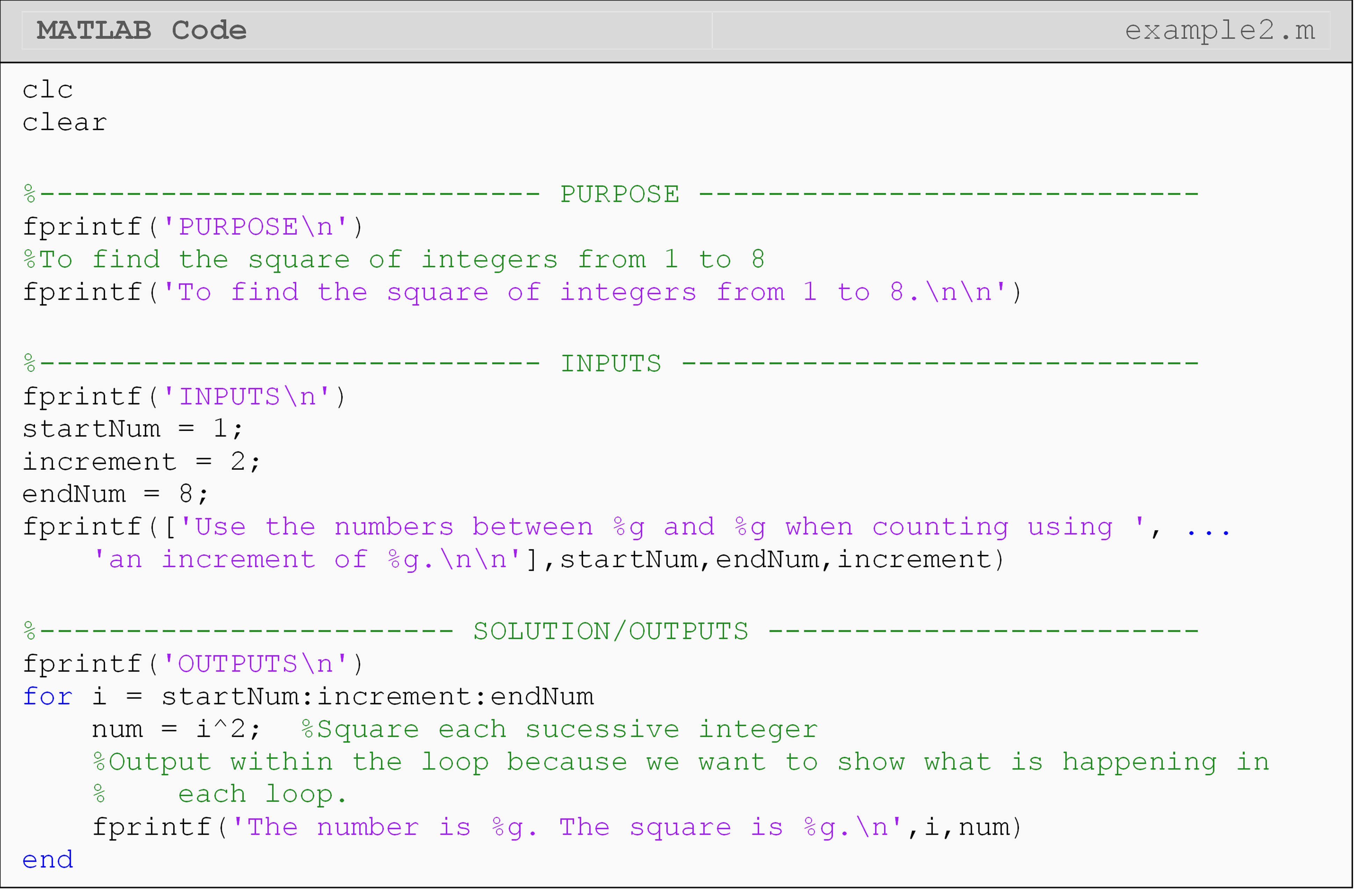
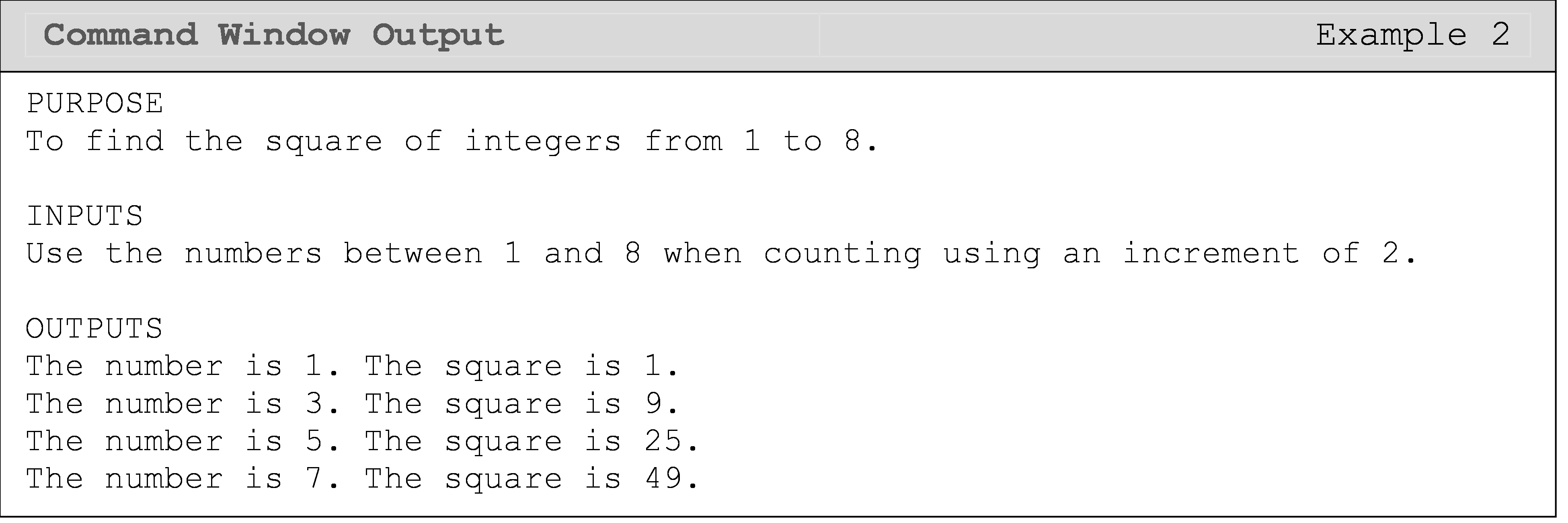
In Example 2, the range of values of the loop counter variable i starts
at 1 and ends at 8. Why does this for loop stop at i = 7? The answer
lies in the increment of the loop counter. This program specifies that
the increment is 2, thus MATLAB starts with i = 1, followed by
i = 3, 5, and finally 7. The next value that i would take on would
be 9, but this is greater than the end value of 8. Hence, 7 is the final
value of the loop counter variable.
How can I reference vectors inside of a loop?
With loops, the possibilities are endless! Any task that needs to be conducted more than once is an ideal job for a loop. In engineering, mathematics, and science, loops are often used to manipulate arrays, find the value of a series or generate a term of a sequence, solve differential equations numerically, find an integral numerically, and many more tasks.
Example 3 shows how loops are used to conduct a mathematical operation: summing a vector of numbers. To do this, we will combine two important concepts we have learned. We have referenced specific elements of a vector before (e.g., vec(1)), but to find the sum of a vector of any size, we need to use a loop to “loop through” all the elements in the vector. Therefore, vec(1)+vec(2)+vec(3)+… becomes vecSum = vecSum + vec(i).
Example 3
Given the following vector data = \[2, 7, 4.5, 2.3, 6, 5\], find the sum of all the elements by using a for loop.
Output the value of the summation by using fprintf(). Be sure to develop a loop that will work for any size vector.
Solution
Pseudocode for Example 3:
\(\;\;\;\;\;\;\;\;\;\) 1. Clear Command Window and all variables.
\(\;\;\;\;\;\;\;\;\;\) 2. Prompt user to input data set, as a vector.
\(\;\;\;\;\;\;\;\;\;\) 3. Use length() to find the number of elements.
\(\;\;\;\;\;\;\;\;\;\) 4. Initialize the loop counter variable used for the summation.
\(\;\;\;\;\;\;\;\;\;\) 5. Start loop.
\(\;\;\;\;\;\;\;\;\;\) 6. Index from 1 to final element number.
\(\;\;\;\;\;\;\;\;\;\) 7. Add each element together in the body of the loop.
\(\;\;\;\;\;\;\;\;\;\) 8. End loop.
\(\;\;\;\;\;\;\;\;\;\) 9. Display results.
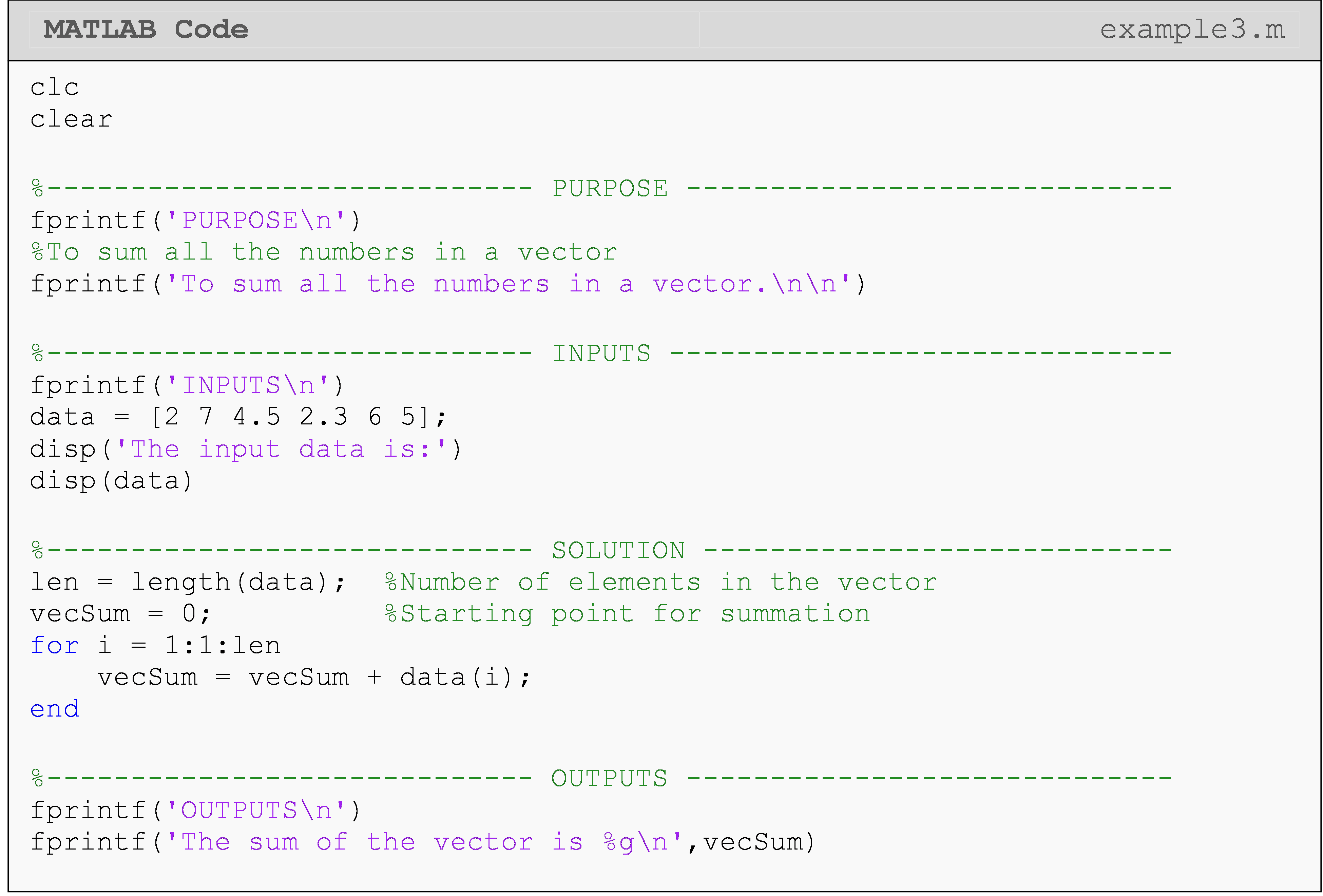

In the m-file, note that the variable named dataSum is equal to zero before starting the loop. Why does the m-file require that dataSum be equal to zero before even starting the loop? Well, think back to the fundamentals of programming. When MATLAB sees a variable name, it asks what its value is. Therefore, when MATLAB evaluates the line dataSum = dataSum + 1 for the first time (i=1), the dataSum on the right side would be undefined (if we had not initialized it). This, of course, will give an error. That is why we initialize dataSum = 0 before the loop starts: so MATLAB will know the value of dataSum on the first iteration of the loop. Once the loop finishes the first repetition, a new value of dataSum overwrites the previous value stored in dataSum, and this continues till the loop has run its course.
Example 4
Background: A legend says that King Shriham of India wanted to reward his grand minister, Ben, for inventing the game of chess. There are 64 squares on a chessboard. When asked what reward he wanted, Ben asked for one grain of rice on the first square of the board, two on the second square of the board, four on the third square of the board, eight on the fourth square of the board, and so on until all squares are covered. That is, he was doubling the number of grains on each successive square of the board. Although Ben’s request looks less than modest, King Shriham quickly found that the amount of rice would be many times more than his country could ever produce. Can you find out how much rice Ben was asking for?
Specifications: Write a program that uses a loop to calculate the total amount of rice on the first n squares of a chessboard given the above scenario. Hint: if four squares on the board are used, then you have eight grains on the last square, and the total grains of rice is 1 + 2 + 4 + 8 = 15.
The program input is the number, \(\text{n}\text{\ (}\text{n} \leq \text{64)}\), of squares used.
The outputs are,
\(\;\;\;\;\;\;\;\;\;\) 1. the number of grains on the last square used that reads: The total number of grains on square ??? is ???“.
\(\;\;\;\;\;\;\;\;\;\) 2. the number of grains of rice on the board that reads: The total number of the grains is ????.
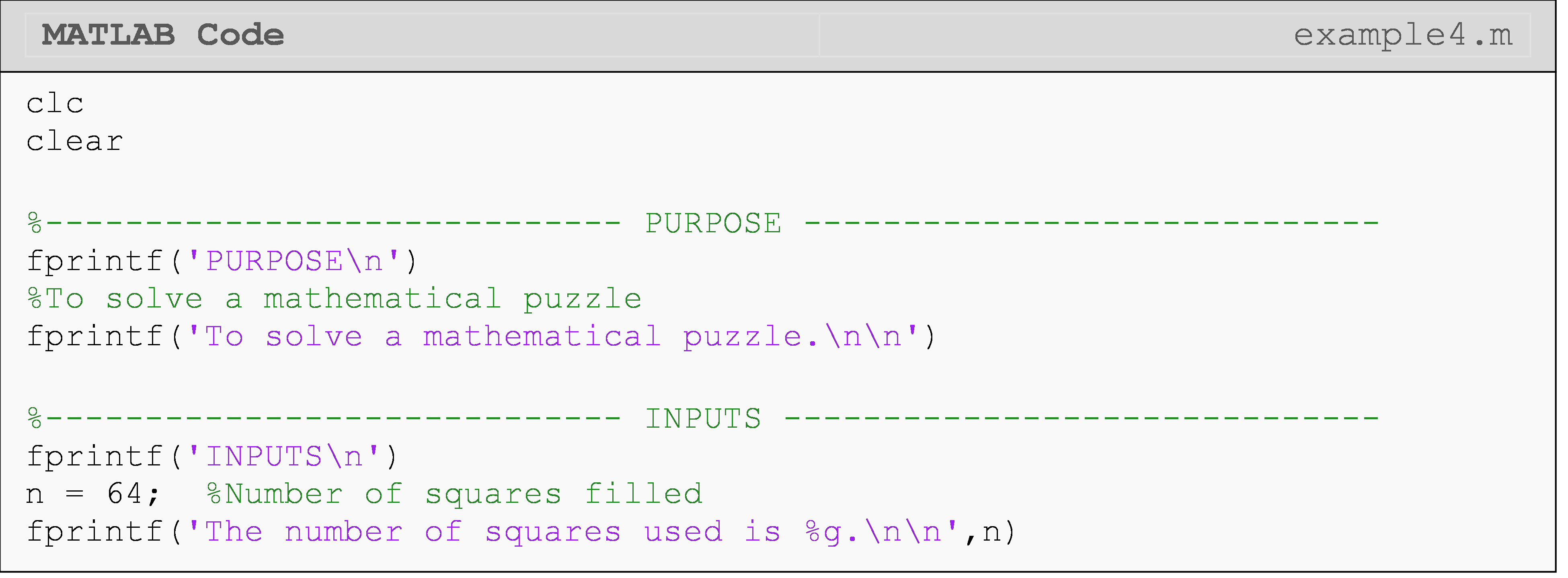
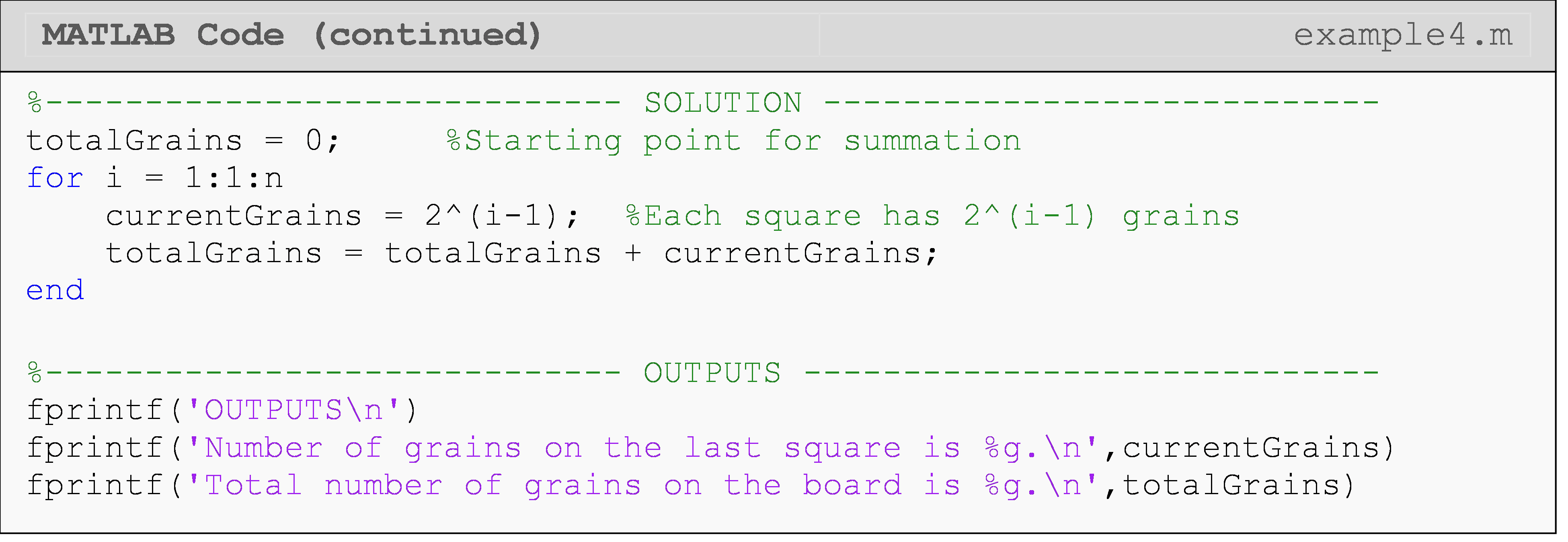

The grains on the current square is assigned to the variable currentGrains. The variable currentGrains is added to the totalGrains to keep track of the grains on the board.
Do I have to use the loop counter variable in the body of the loop?
No, you do not have to use the loop counter variable in a for loop. The purpose of the loop counter variable and its assignment in the for loop is to control the number of times the loop will repeat itself.
One can see that in the solution in Example 5, the loop counter variable j is not used in the body of the for loop. In this case, the loop counter variable is solely used as a counter, to keep track of how many repetitions that this loop has made.
Example 5
You can find the square-root, \(x\), of any positive real number, \(R\), by using the recursive formula given as
\[x_{i+1} = \frac{1}{2}\left ( x_i +\frac{R}{x_i} \right )\]
Write a for loop to find the value of \(x\) for \(R = 9\), which is updated
recursively by \(\frac{1}{2}\left ( x + \frac{9}{x} \right )\). Use a starting
value of x = 64 and do the recursion 10 times.
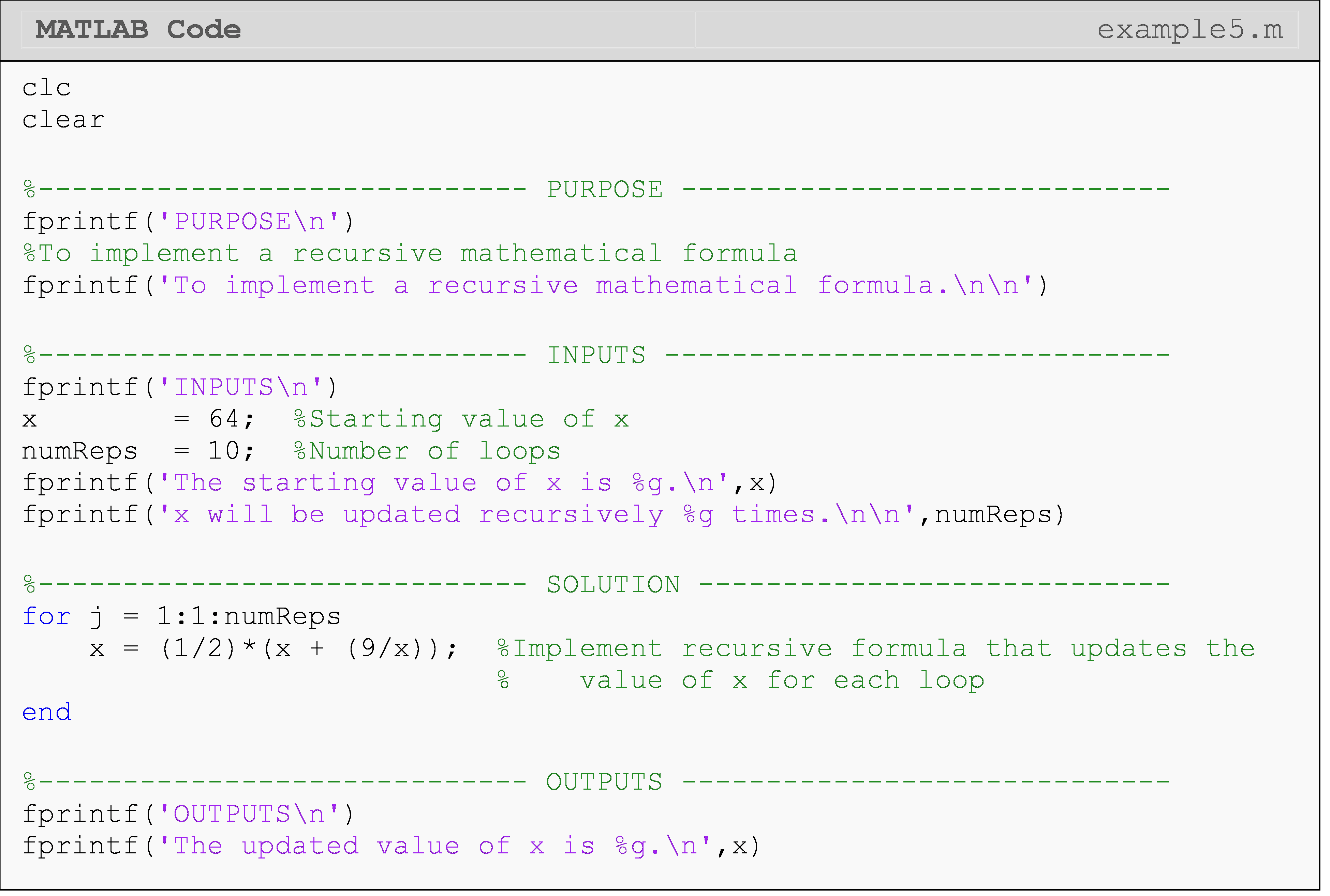
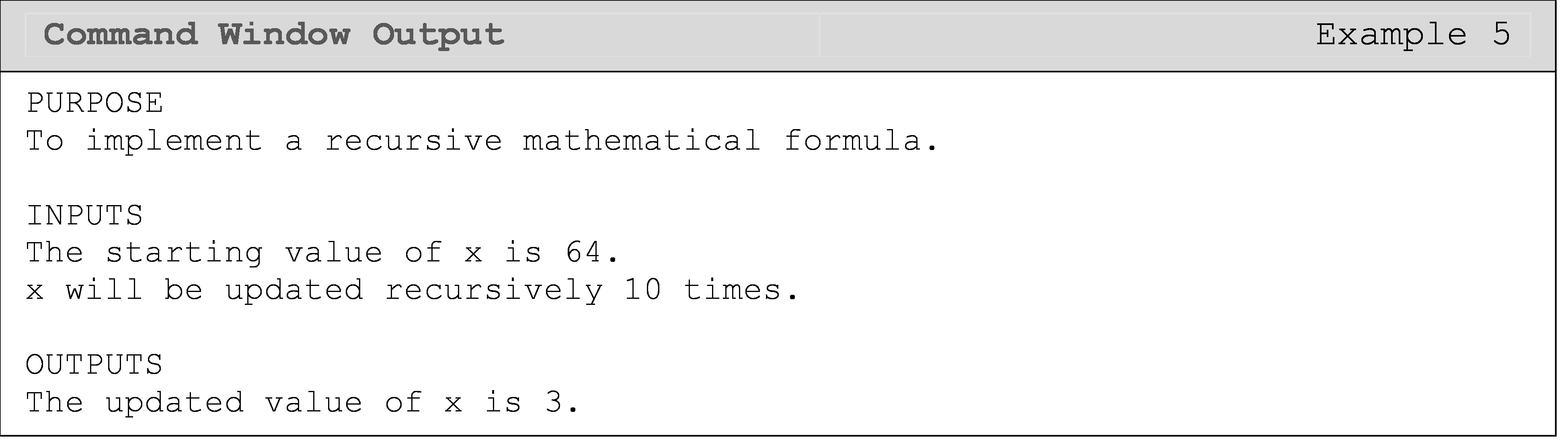
To review, all for loops require a loop counter variable assigned to a
vector of startingValue:increment:endValue, a body of code, and an end
statement. The loop counter variable does not need to be used inside the
loop (recall Example 5) because it is just a counter to keep track of
repetitions.
When do I use a for loop vs. a while loop?
There are no absolute rules for when to use a
for loop over a
while loop or
vice versa. In almost every case, you can accomplish the task with
either a for or a
while loop (this
is because you can use conditions to change the behavior of a
for loop into a
while-like loop). The difference is the efficiency or elegance of your
solution. There is generally no right answer, so you should focus on
learning how each one works rather than when to use each one.
Examples 6 and 7 are given purely to demonstrate the similarities
between using a
for and
while loop to
solve the same simple problem. As mentioned above and in later lessons,
there are cases where one is easier and more appropriate to implement
than the other.
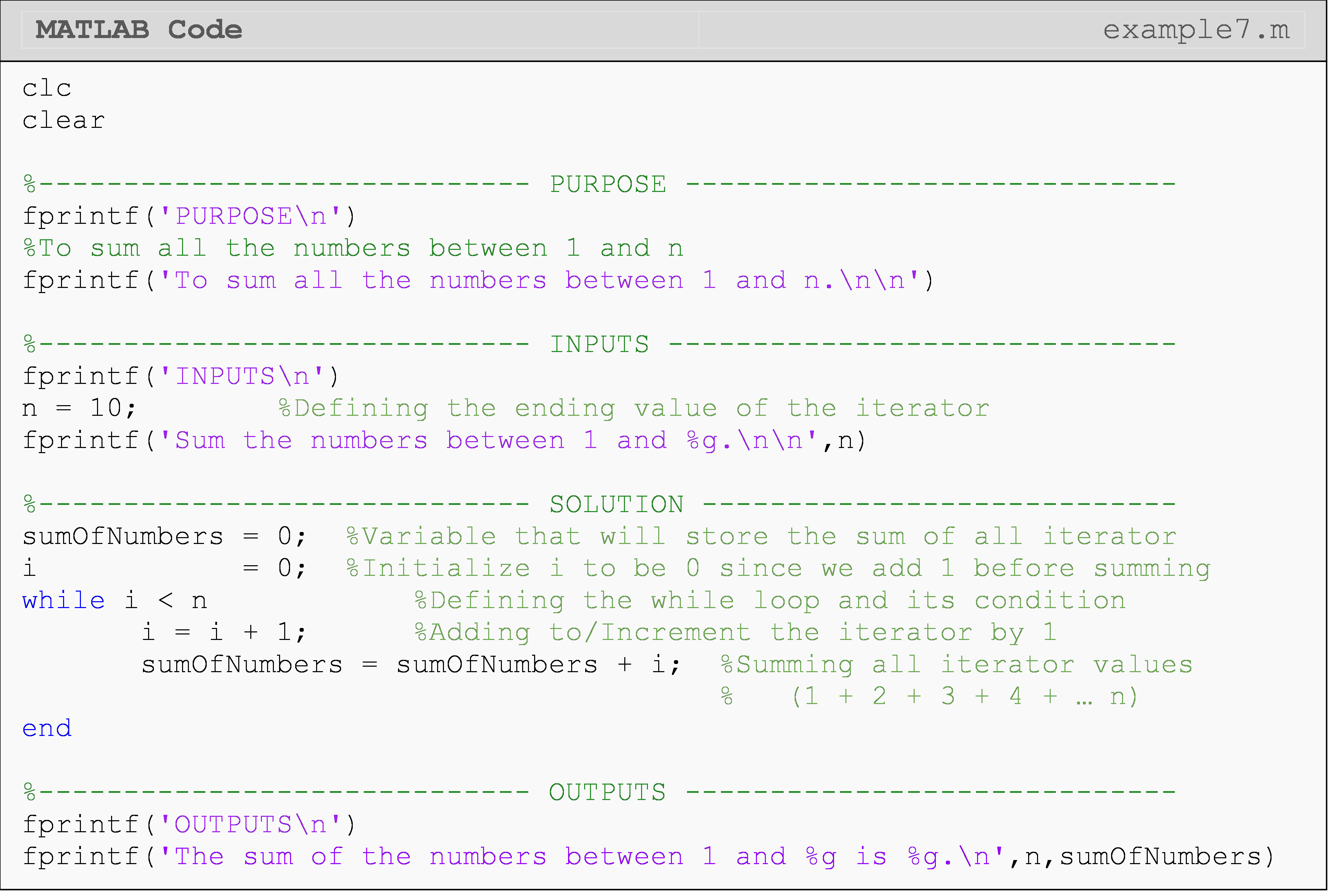
Example 6
Write a program that sums all the numbers between 1 and n using a for
loop. Display the final sum in the Command Window. Use n = 10 as a test
case for the program.
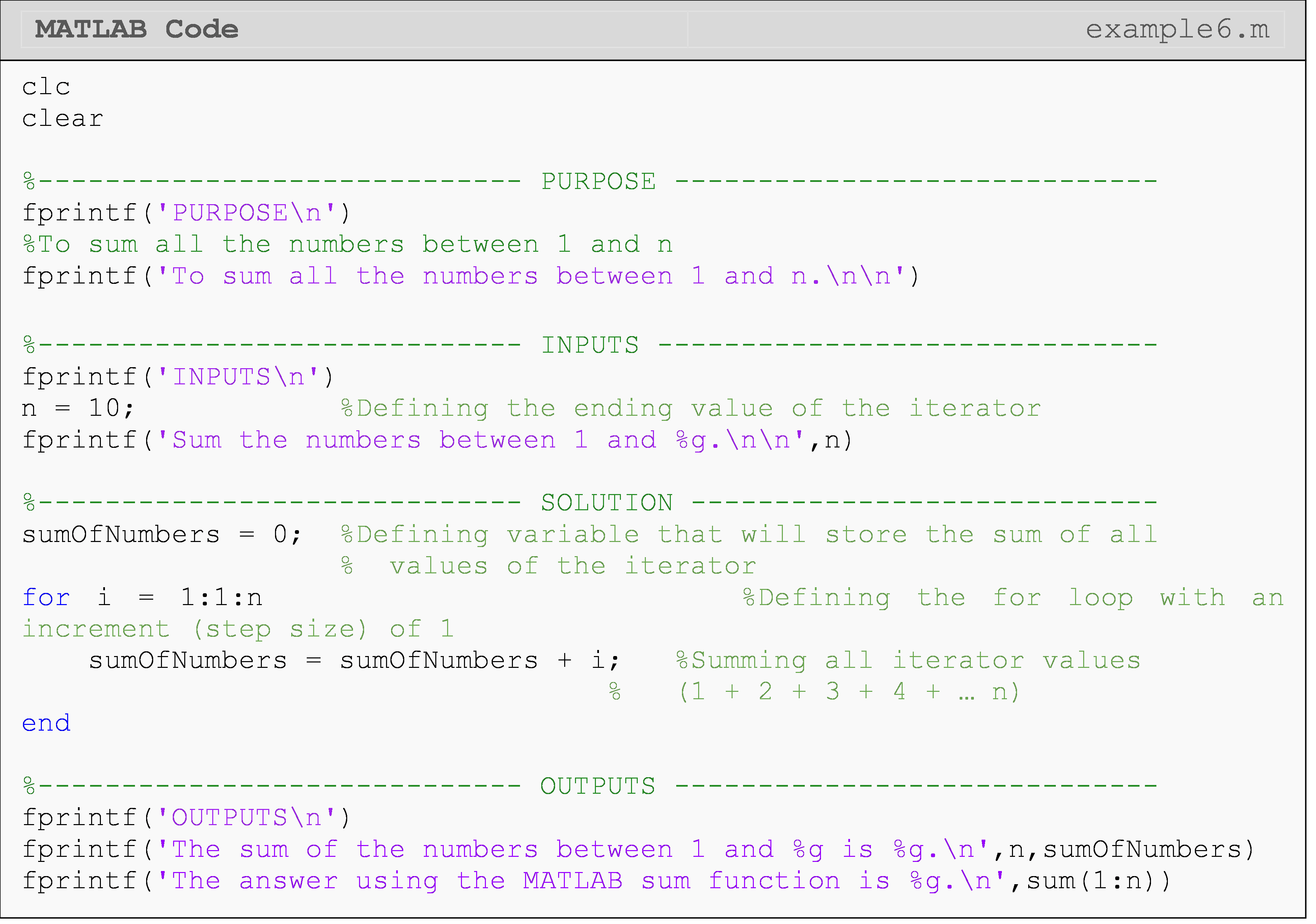

Remember, it would be wrong to name “sumOfNumber” as “sum” since “sum”
is a predefined MATLAB function. If it was named “sum”, the actual
function “sum()” would be redefined, and would not work in the final
fprintf() function.
Now, we can solve the same problem using a
while loop. We
achieve the same answer in both Examples 6 and 7.
Lesson Summary
| Task | Syntax | Example Usage |
|---|---|---|
| Iterate over a block of code definitely | for |
for a = 1:5; disp(a); end |
Problem Set
(1). Write a program using a for loop that adds the number 7 to each
value of j, as j takes on integer values of 1,2,…,11,12. Output
all 12 values to the Command Window.
(2). Write a program using a for loop that adds the number 7 to each
value of j, as j takes on integer values of 12,11,…,2,1. Output
all 12 values to the Command Window.
(3). Using loops, write a program that adds the number 7 to each value of
j, as j takes on integer values of 1, 3, …,9, 11. Output all
values to the Command Window.
(4). A function \(f(x)\) is calculated by using the following infinite series,
\[f(x) = \frac{1}{3} + x + x^{2} + x^{3} + x^{4} + ...\]
Complete the following:
(a) Use the syms command with x as the symbolic character to show the
series in the Command Window. The only program input is the number
of terms to use, n.
(b) Calculate the value of \(f(x)\) using an \(x\) value of 1.24 and the first 30 terms of the infinite series.
(5). The function, \(cos(x)\) can be calculated by using the following infinite Maclaurin series
\[\cos(x) = 1 - \frac{x^{2}}{2!} + \frac{x^{4}}{4!} - \frac{x^{6}}{6!} + .....\]
The absolute percentage relative approximate error \(|\varepsilon_{a}|\) is defined as
\[|\epsilon_{\text{a}}| = \left| \frac{\text{Present Approximation} - \text{Previous Approximation}}{\text{Present Approximation}} \right| \times \text{100.0}\]
(a) Find \(cos(0.5)\) using five terms of the series.
(b) Find \(cos(0.5)\) using six terms of the series. Find the absolute percentage relative approximate error at the end of using the six terms.
(6).Find the average and standard deviation of a given vector of numbers. The average of numbers \(\left( x_{1},x_{2},x_{3},...,x_{n} \right)\) is given by
\[\overline{x} = \frac{\sum_{i = 1}^{n}x_{i}}{n}\]
and the standard deviation of the numbers is given as
\(\sigma = \sqrt{\frac{\sum_{i = 1}^{n}\left( x_{i} - \overline{x} \right)^{2}}{n - 1}}\).
Write a program using for loops to find the average and the standard
deviation of given numbers in a vector.
(7).The function \(f(x)\) is calculated by using the following infinite series,
\[f(x) = \frac{x^{2}}{17} + \frac{x^{3}}{3} + \frac{x^{4}}{3} + \frac{x^{5}}{3} + ...\]
Complete the following:
(a) Write a pseudo code for a MATLAB function that finds the value of \(f(x)\), given the number of terms to use, \(n\) and the value, \(x\).
(b) Write a MATLAB function my_fun using for loops for calculating
\(f(x)\). Use \(n\) terms to calculate \(f(x)\) at a given value of
\(x.\)
\(\;\;\;\;\;\;\;\;\;\;\)function fn=my_fun(x,n)
(c) Test the function in a separate m-file for four different cases of input variables:
\(x=0.25\), \(n=4\)
\(x=0.25\), \(n=61\)
\(x=3.00\), \(n=1\)
\(x=3.00\), \(n=2\).
(8). Using your knowledge of for loops and/or conditional statements,
write a MATLAB program that outputs the factorial of any positive
input integer N. Recall that the factorial of a number is found as
\(n! = n \times (n - 1) \times ... \times 2 \times 1\).
For example,
\[\begin{split} 5! &= 5 \times 4 \times 3 \times 2 \times 1 \\ &=120\end{split}\]
Also, recall that 0! is explicitly defined as equal to 1. Provide an error message in the Command Window if the input number is negative or not an integer. You should not use the factorial() or similar function to complete this problem.
Test run your program with two sets of inputs. First, test run your program with the following input,
n = 8
where the output would be
8! is 40320
Then, test run your program with the following input,
n = -12
where the output would be
Error -- The input is negative
Lastly, test run your program with the following input
N = 12.3
where the output would be
Error -- The input is not an integer
(9).A prime number is a positive whole number which has exactly two
distinct number divisors. In other words, a prime number is only
divisible by itself and 1. For example, 2, 3, 5, 7, 11, 13 are
prime numbers. Note that the number 1 is not a prime number. Use
your knowledge of for loops and/or conditional statements to write
a MATLAB program that determines if an input positive whole number
is a prime number. The program input is any positive whole number,
n (\(n \geq 1\)), and the program output is whether or not the
inputted whole number is a prime number.
Test your program for the number 97, which is a prime number.