Module 1: INITIAL SETUP AND BASIC OPERATION
Learning Objectives
After reading this lesson, you should be able to:
use the Command Window and understand its function,
control what appears in the Command Window,
access MATLAB documentation through the Command Window.
What is the Command Window and how can I use it?
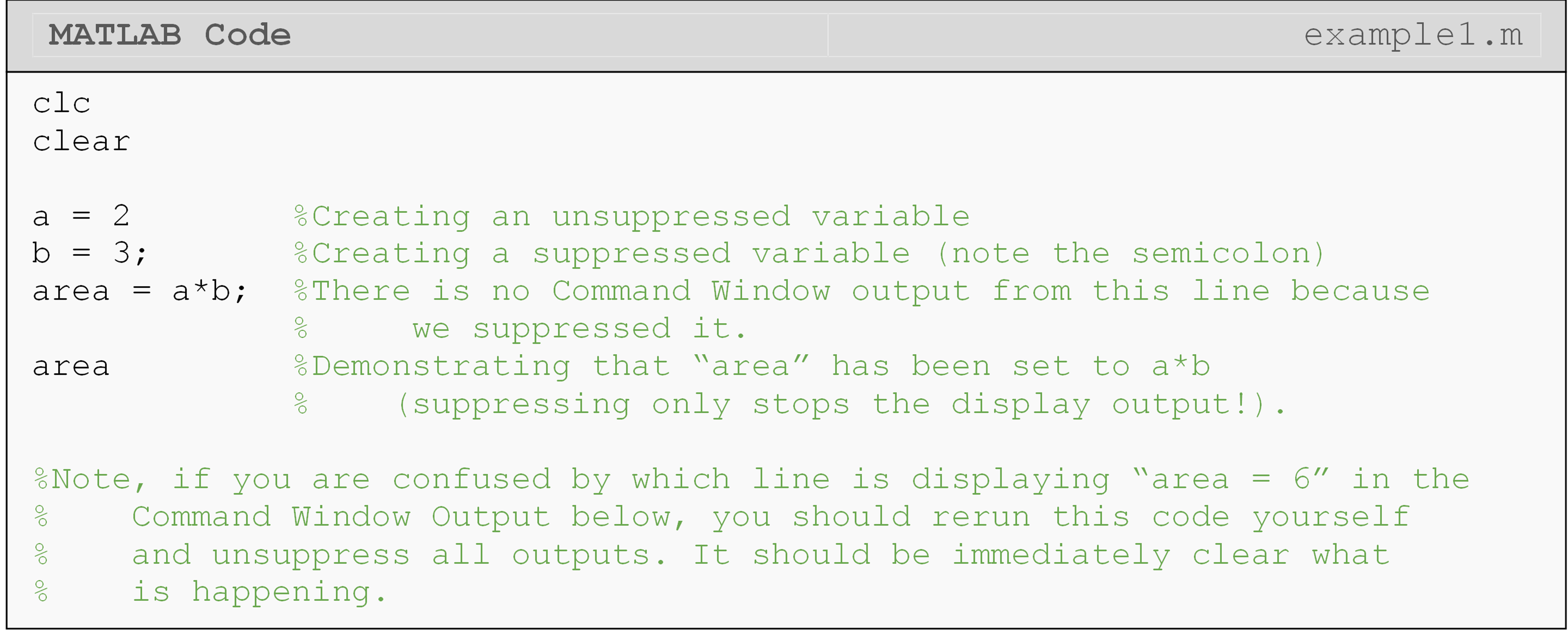
The Command Window (Figure 1) is the main window used to display the program output in MATLAB. We can also program directly into the Command Window; however, our code will not be saved in an m-file.
Figure 1: The default MATLAB window configuration is shown with m-file open. The Command Window is at the bottom center.
Table 1: Commonly used mathematical operators.
| Operation | Syntax |
|---|---|
| Add | + |
| Subtract | - |
| Multiply | * |
| Divide | / |
| Power | ^ |
| Square Root | sqrt() |
This means you can quickly test a few lines of code, use it as a
calculator, or check the value of a variable (see Figure 2). This also
means it can be a useful tool when debugging (find errors in the code)
in your program. To use basic mathematical operators and numerals, just
input the statement and hit the enter key. Table 1 shows a few common
mathematical operators commonly used in MATLAB. Note that when the
answer is displayed, it is assigned the name, ans, by default.
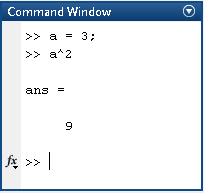
Figure 2: Command Window used for a quick calculation (left), outputting the value of a previously defined variable (middle), and a quick and small program (right).
It is important to note that MATLAB does not understand what an equation
is as known to you in a traditional sense. In MATLAB there is a variable
name side and an expression side to any statement, and these sides are
divided by an “equal to” sign. The variable name is always on the left
side and the expression is always on the right side of an equal to sign.
How this works is that MATLAB reads a variable name and attaches that
variable name to what is on the right side of the equal to sign. This
variable name is now associated with the number or expression on the
right side of the equal to sign. If you do not assign the expression to
a variable name, then MATLAB automatically assigns a default name,
ans, to the expression.
How can I suppress outputs in the Command Window?
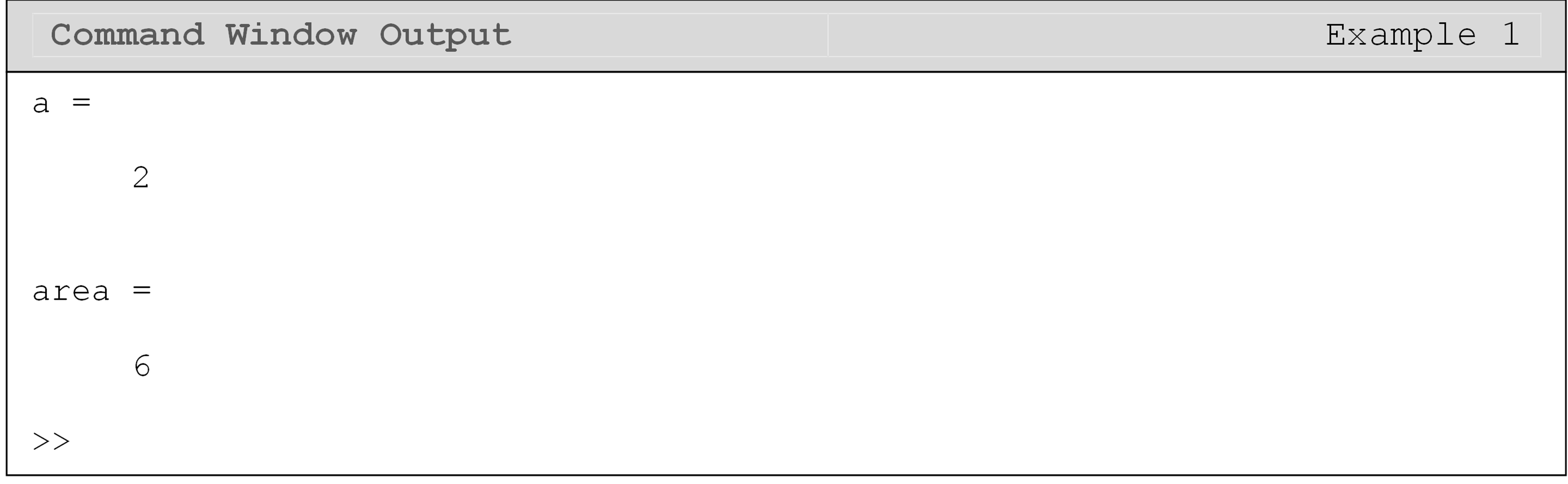
The Command Window will display the outputs of all executable code that is in the m-file. In most cases, the programmer may only want the final solution to be displayed, suppressing outputs of all other lines. Suppressing variables can also decrease the run time of your program (if it is long). To make this possible, MATLAB has a special character that can be added to any line of the m-file – the suppression character. This suppression is made possible by inserting a semicolon (;) at the end of any line of code. It is important to note that although the output of a line followed by the semicolon (;) is not displayed in the Command Window, the calculation in the line is still being done “behind the scene” by MATLAB. An example of using this character to suppress outputs from the Command Window is shown in Example 1.
Important Note: Suppressing a line
of code will only change whether it outputs to the Command Window or
not: it does not stop MATLAB from performing the operation.
Can I view help from the Command Window?
If you cannot remember syntax/usage while you are programming, the
help and
doc commands can
be used directly in the Command Window to pull up documentation on a
specific MATLAB function or command.
The difference between
help and
doc is that
help contains a
summary of the documentation and displays directly in the Command Window
(see Figure 3) while
doc opens a new
window with the full documentation page from MathWorks. Both are quick
and easy ways to review documentation.
Can the Command Window do it all?
The Command Window does have limitations. In fact, it is rarely used to perform mathematical operations or for doing MATLAB programming. The main reasons for this are that it is difficult to change expressions without overwriting them and displaying useful information in the Command Window is cumbersome. For the purposes of this book, the main role of the Command Window is to only display the output information from a MATLAB file (also called an m-file). Although it is important to understand the inner workings of the Command Window, the m-file is the basis of MATLAB programming as described in Lesson 1.5.
Figure 3: Using the
help command to
retrieve documentation from the Command Window.
Lesson Summary of New Syntax and Programming Tools
| Task | Syntax | Example Usage |
Suppress an output (Command still processed) |
; |
code; |
| Get summary of documentation for a MATLAB command or function | help |
>>help disp |
| Open documentation page for a MATLAB command or function | doc |
>>doc disp |
| Add two variables | + |
a+b |
| Subtract two variables | - |
a-b |
| Multiply two variables | * |
a*b |
| Divide two variables | / |
a/b |
| Raise a variable to a power | ^ |
a^2 |
| Take the square root of a variable | sqrt() |
sqrt(a) |
Multiple Choice Quiz
(1). The MATLAB syntax to suppress output from the Command Window is
(a) %
(b) &
(c) supp(' ')
(d) ;
(2). Using the Command Window, 2^(4^2) will give the following output
(a) 16
(b) 256
(c) 512
(d) 65536
(3). Using the Command Window, 2^4^2 will give the following output
(a) 16
(b) 256
(c) 512
(d) 65536
(4). In the Command Window, if we enter:
>>d = 5;
>>a = d^2
then the output of the last line is
(a) 5
(b) 10
(c) 25
(d) Undefined function or variable 'd'.
(5). In the Command Window, if we enter:
>>a = 5;
>>a = 6;
>>a
then the output of the last line will be:
(a) 5
(b) 5.5
(c) 6
(d) 11
Problem Set
Use the Command Window to complete the following exercises.
(1). Find the output of \(b\) given that \(a = 6\) and \(b = 12a\).
(2). Using Ohm’s law,
\[V = i \times R\]
find the electrical current \(i\) passing through a resistor of resistance \(R=2 \times 10^{3}\ \Omega\), and a voltage potential \(V=12\text{ V }( \text{DC})\).
(3). Find the area (\(\text{in}^2\)) of a right-angled triangle that has a base measurement of 4 inches and an adjacent angle of \(32^{\circ}\).
(4). Find the lift force in Newtons of an airfoil at a constant velocity (V) of 35 m/s, and in a fluid environment with a density (\(\rho\)) of \(1.247\ \text{kg/m}^3\). The airfoil has an exposed area (\(A_{exp}\)) of \(2451\text{ cm}^{2}\) and the coefficient of lift is found to be 0.81. For your solution, you may use the formula for the lift force as:
\[\displaystyle F_{\text{Lift}} = \frac{1}{2}\rho A_{\text{exp}} C_{\text{lift}} V^{2}\]
(5). Redo exercise 4 as follows. Find the lift force in Newtons using the same fluid density, exposed area, and lift coefficient as stated in Exercise 4, but choose the velocity first to be 25 m/s and then to be 50 m/s. Note that the values of fluid density, lift coefficient, and exposed area are already stored in MATLAB.