Module 4: MATH AND DATA ANALYSIS

Lesson 4.2: Symbolic Variables

Learning Objectives

After reading this lesson, you should be able to:

use symbolic variables in MATLAB to form equations,
substitute a number or variable into a symbolic expression,
convert symbolic variables to other data types.

What is a symbolic variable?

A symbolic variable does not have a numerical value assigned to it. Use the following function as an example $f(x)= x^2$; where the symbolic variable is $x$. The value of $x$ has no numeric value assigned to it; therefore, it is a symbolic variable.

The symbolic toolbox introduces syms: a new data type. syms allows you to create variables without assigning them a value (number, string, etc.). This is very useful when doing anything beyond the basic “2+2” math. Solving equations, calculus, and differential equations are a few examples of how syms is used to solve mathematical problems, and it demonstrates part of the functionality of the MATLAB symbolic toolbox.

What is a MATLAB toolbox?

A MATLAB toolbox, more traditionally referred to as a package or library in other programming languages, is just a set of code (which you do not need to see) that gives you more predefined functions. We have been using functions all along, but have not talked explicitly about a “toolbox” because we have used pre-installed, default functions. One example is the plot() function. MATLAB knows how to plot the data you input to the function because there is an algorithm doing the work for you behind the scenes. We will learn how to write our own functions and reference them in Module 7.

How do I use symbolic variables?

To use a symbolic variable in MATLAB, you use the syms command. This command needs to be placed before the symbolic variable that is intended to be used in an expression. Otherwise, MATLAB will return an “undefined variable” error. The syms command tells MATLAB to treat a specified variable as symbolic (it has no value). Note that symbolic variables must follow the same naming rules as all other variables (reference Lesson 2.1 for naming rules).

If more than one symbolic variable is required, the variables can be made symbolic by using the syms command by separating each symbolic variable by a space. Look at Example 1 to see the syms command in action.

Example 1

Given two functions $y(t)$ and $z(t, x)$, $y = {t}^{2} + {2}{t}$ and ${z} = \displaystyle\frac{tx+1}{x^2}$, use the syms command and display each function in the Command Window.

Solution

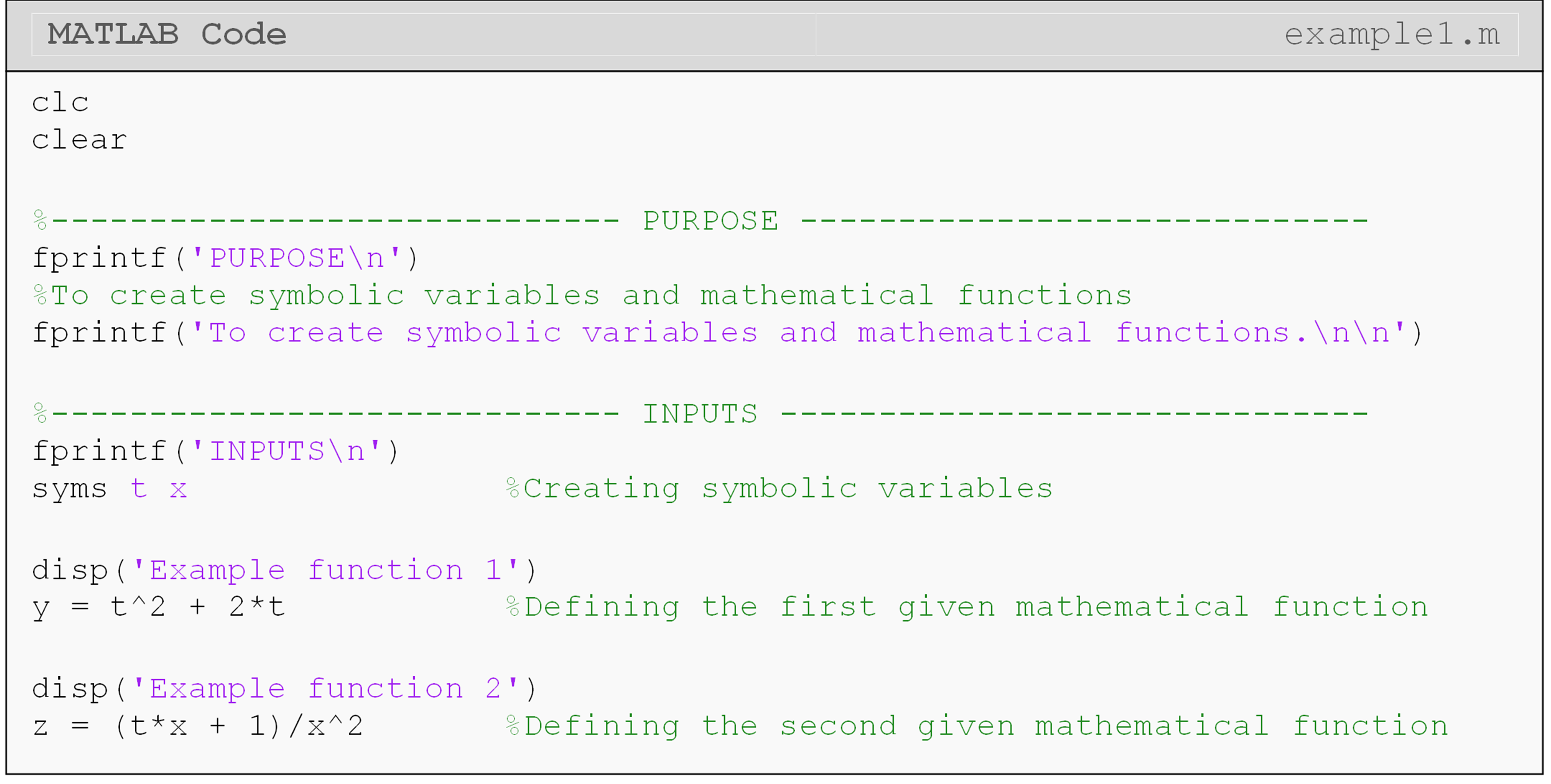
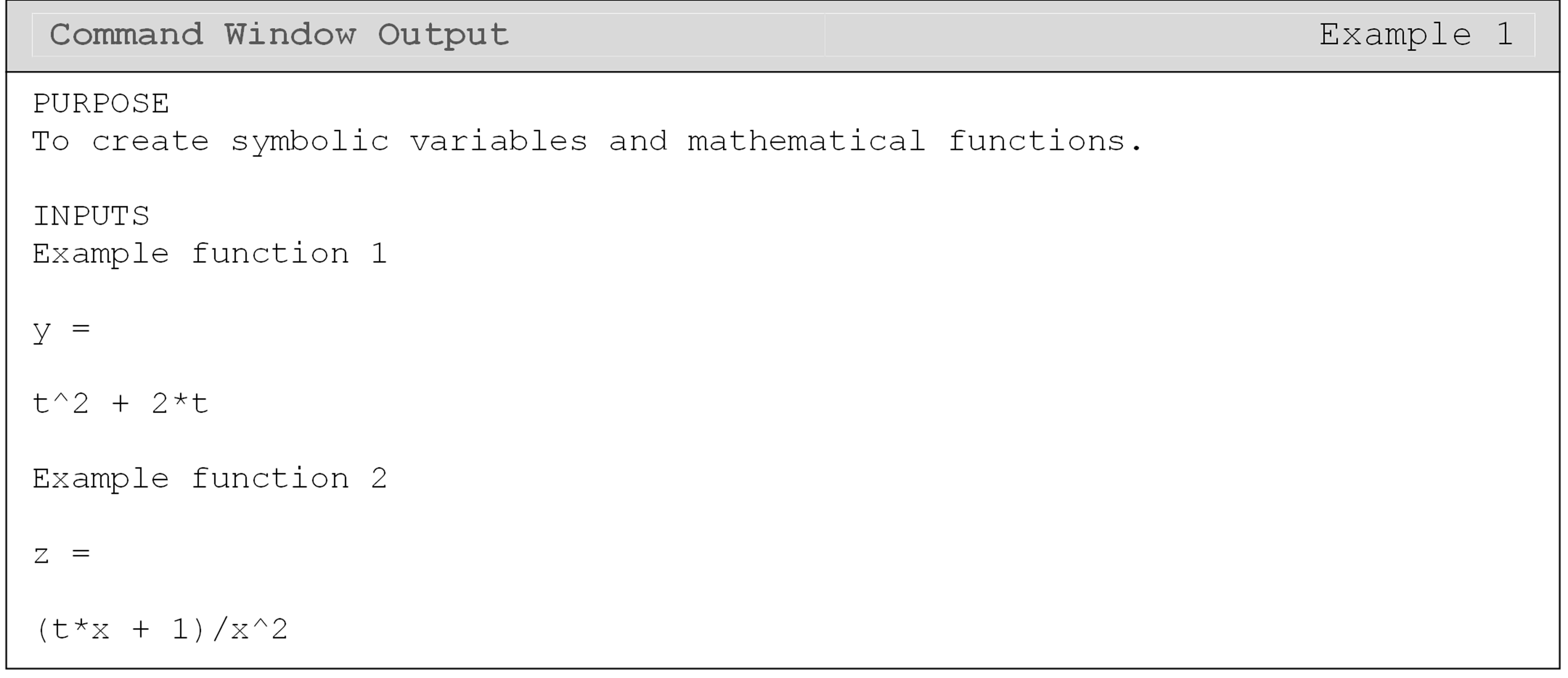
Example 1 shows the syms command being used to make two variables, $t$ and $x$ symbolic. These symbolic variables are then used to generate the mathematical functions $y$ and $z$. The Command Window output shows the two specified functions being output to the Command Window (they were not suppressed). Another way to direct output mathematical functions containing symbolic variables is to use the use the disp() function (e.g., disp(y)).

How do I clear specific variables?

To make a variable no longer symbolic, the clear command is used. You may recall that the first two lines of most m-files should be clc and clear. We know that using clear will clear all of the MATLAB variables stored from the current workspace, which essentially means that all the variables you defined. However, you may also specify precisely which variable(s) to clear by using the clear command followed by the variable names. For example, clear x would clear the variable x from memory, and clear myVar would clear the variable myVar from memory. Note that clearing a symbolic variable is application-specific and not mandatory.

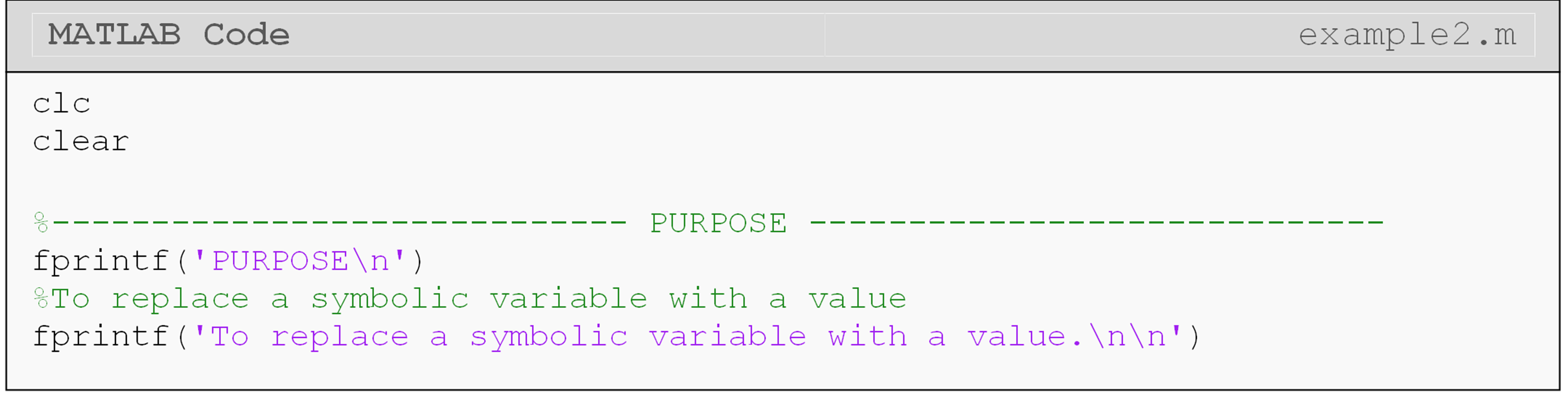
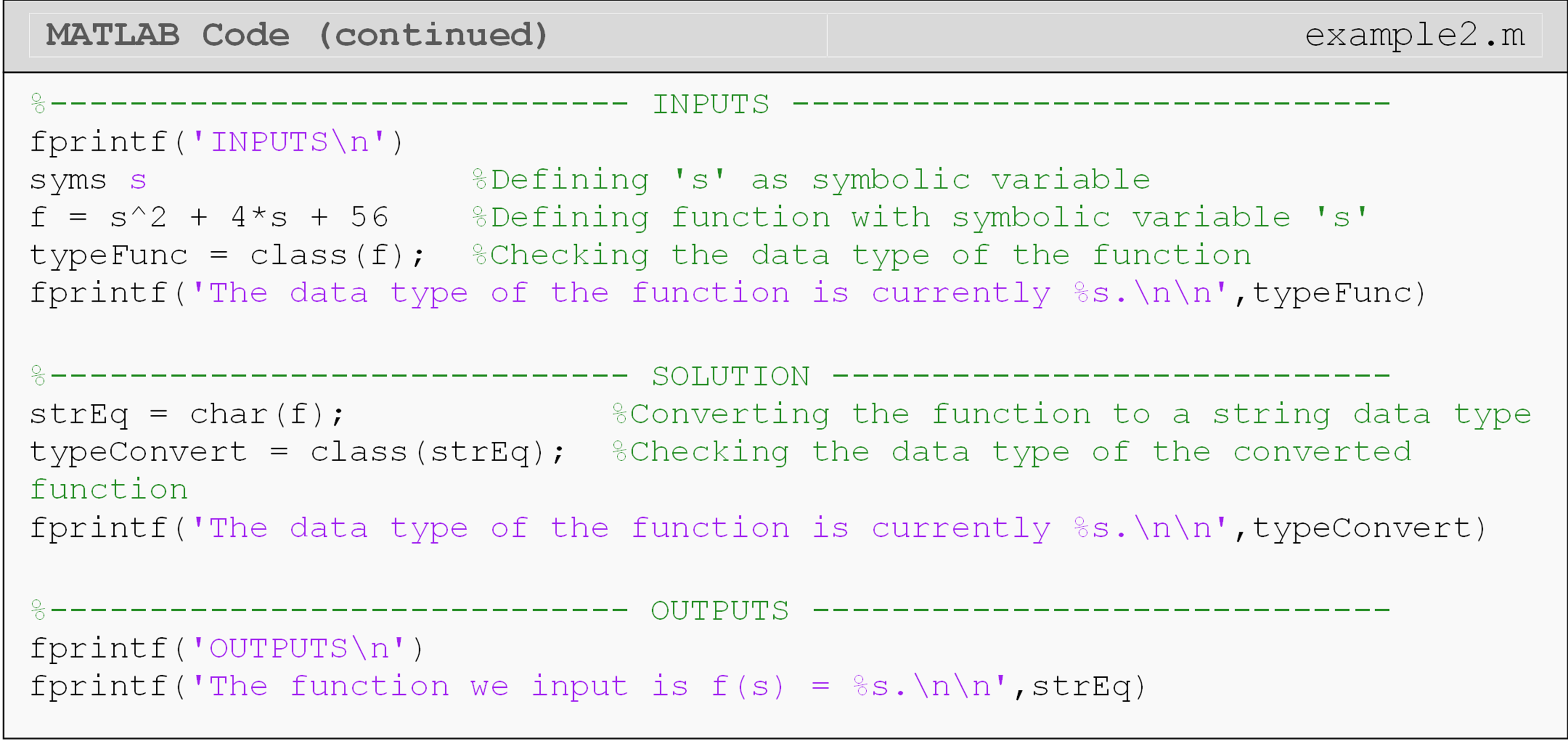
How can I convert from syms data type to other data types?

Since syms is a data type in MATLAB, it often needs to be converted to a different data type, such as double or char, to display it. See Example 2 for some specific use cases. Using the wrong conversion could result in an error. Some commonly used functions to convert the syms data type to other data types/formats are:

double() - > Convert a symbolic matrix with numerical value to MATLAB numeric data type.
char() - > Convert symbolic objects to strings.

Example 2

Input the function $f(s) = s^2 + 4s + 56$ to MATLAB, convert it from sym data type to char data type. Then output the converted function using fprintf().

Solution

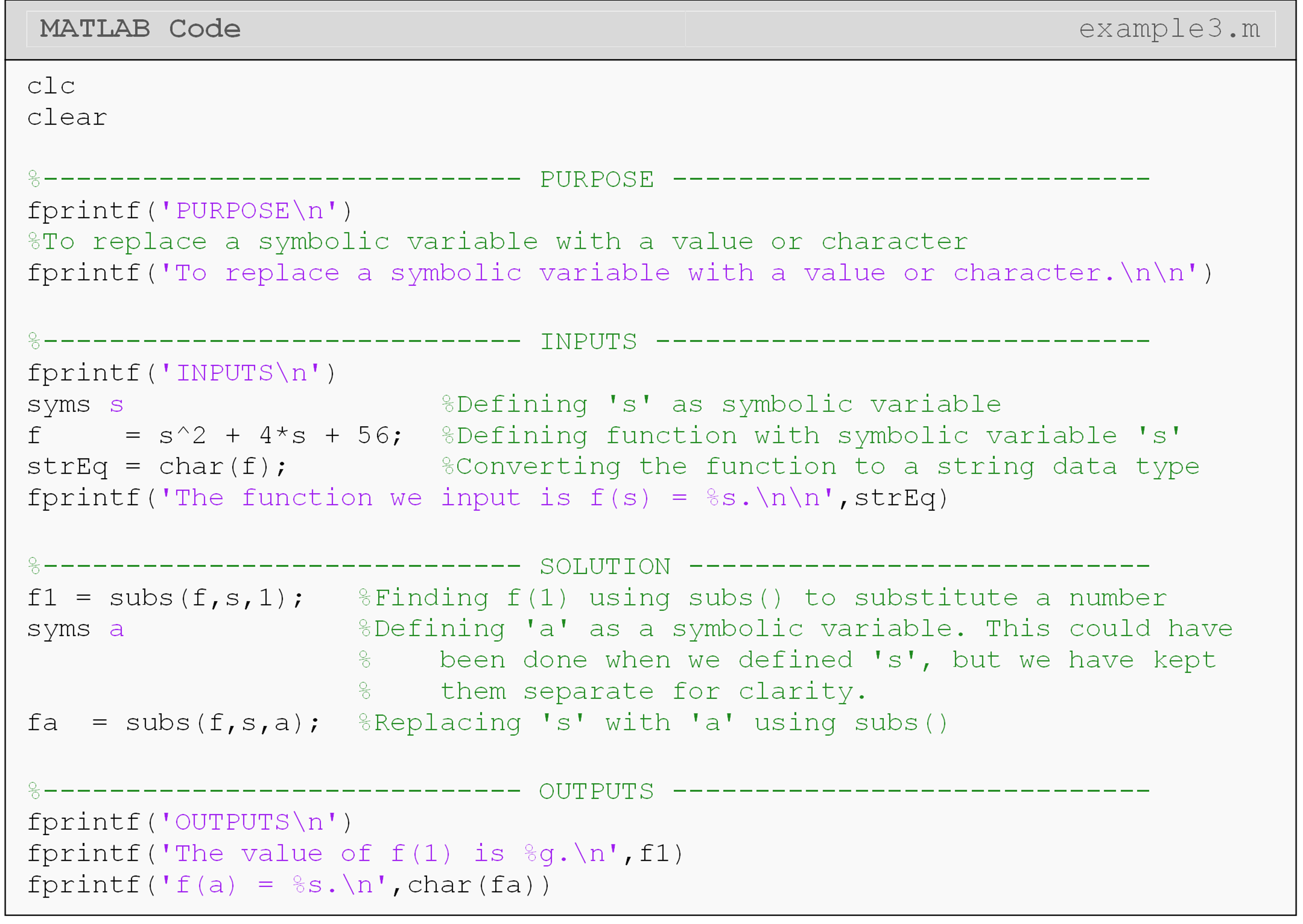
Can I replace a symbolic variable with a value?

MATLAB makes changing/substituting the value or the name of a symbolic variable simple. Using the subs() function, you can assign a value for the symbolic variable (e.g., $x = 1$) or rename it (e.g., $x = a$). This function is handy when we plot equations later in this lesson and in future lessons.

Example 3

Find the value or form of the function $f(s)=s^2 + 4s + 56$ at $s=a$ and $s=1$.

Solution

How can I change the output format of syms?

You can change the output type (scientific, floating-point, etc.) directly within an fprintf() function if your number is in decimal form. However, MATLAB returns exact solutions by default; that is, it will return “1/3” instead of “0.33333…”. The precision of an answer can be adjusted using the function vpa().

This is sufficient for most purely numerical answers. If you have an answer that contains symbolic variables like x, t, etc., you may need to use the function simplify() to help clean up and simplify messy solutions.

Lesson Summary of New Syntax and Programming Tools

Task	Syntax	Example Usage
Create a symbolic variable	`syms`	`syms x`
Convert a variable (with numeric value) to double precision (numeric data type)	`double( )`	`double(var)`
Convert a variable to the char data type	`char( )`	`char(var)`
Substitute a new value or variable for the current symbolic variable	`subs( )`	`subs(eq,replaceVar,newVar)`
Adjust the precision of a numeric variable	`vpa( )`	`vpa(x,3)`
Simplify an algebraic expression	`simplify( )`	`simplify (x)`

Multiple Choice Quiz

(1). If one was going to write $y=3*x$ in an m-file, the variable(s) that would need to be declared as symbolic is (are)

(a) x

(b) y

(d) either x or y

(2). Given the following code:

the output of the last line in the Command Window is

(a) e = 7*c^2

(b) e = m*c^2

(d) Undefined function or variable…

(3). To display the function $f(x) = x^2$ in the Command Window given the program

the correct line of code to add is

(a) fprintf('The function is f(x) = %g.\n',char(f))

(b) fprintf('The function is f(x) = %s.\n',char(f))

(d) fprintf('The function is f(x) = %f.\n',vpa(f))

(4). The symbolic variable that will cause an error when used in an m-file is

(a) ex

(b) sin

(d) x

(5). The Command Window output of the last line of this program is

(a) 3x

(b) 15

(d) Undefined function or variable 'x'.

Problem Set

(1). In a single m-file, display the expression in all the parts below in the Command Window.

(a) $\displaystyle y = \frac{2}{3}x^2+x+x^{\frac{1}{2}}$

(b) $z = \displaystyle \frac{x^2y}{x+1}$

(d) $x =\displaystyle \frac{M_\nu}{M_\nu+M_l}$

(2). In most cases, the weight w of an object is determined by the mass of the object m and the acceleration acting on the body of the object a given by the relationship\[ w=ma \]Display the general expression to find the weight of a body.

(3). Evaluate the following functions. Output both the function and the resulting value from evaluating the functions at the given numbers to the Command Window. You should use a single fprintf() function for each function-value pair of outputs.

(a) Evaluate $f(x)=x^4+98$ when $x = 2$.

(b) Evaluate $G(s)=s^2+5s-6$ when $s = 3.4$.

(4). The brake power of an internal combustion engine is found by\[ P=r*T \]where, P = Power (Watt) r = Rate (radian/sec) T = Torque (N-m) and the engine torque is given by \[ T = 0.62r \]Using MATLAB,

(a) display the general expression for the brake power generated by the engine,

(b) find the value of the brake power when r is 350 rad/sec,

(c) plot power vs. rate with values of r from 0 to 630 rad/sec. Use appropriate labels, title, etc., as required to describe the plot.

(5). The acceleration of a point on a body is composed of four components: the tangential, normal, sliding, and Coriolis. Assuming that sliding and Coriolis effects of acceleration are zero, the tangential $ (a_) $ and normal $(a_{normal})$ components of acceleration can be combined as functions of time, t,\[ a_{total}=\sqrt{a^2_\text{tan}+a^2_{normal}} \]where \[ a_\text{tan}=2\sin \left(\frac{1}{2}t\right)+t^2 \] \[ a_{normal}= \displaystyle \frac{\left(\frac{1}{3}t^3-4\cos(\frac{1}{2}t)\right)^2}{300} \]The units of time are seconds and the units of acceleration are $\text{m}/\text{s}^2$. Display the equation for the total acceleration of the body in the Command Window (use t as a symbolic variable). Find the value of the acceleration of the body when $t = 4.3$ seconds.
Hint: Do not name the variable for the tangential acceleration “atan”. It is a predefined function in MATLAB.