Module 2: BASIC PROGRAMMING FUNDAMENTALS
Learning Objectives
define vectors and matrices in MATLAB,
manipulate vectors and matrices effectively with common MATLAB syntax,
reference strings as vectors (arrays).
Why is the program called MATLAB?
MATLAB stands for Matrix Laboratory, and as the name implies, MATLAB is designed to solve problems using matrices. When MATLAB was originally designed, the basis of the program was to solve all problems using matrix algebra. Even if the user is conducting simple scalar operations, MATLAB will store these scalar values in a matrix of the size \(\text{1}\text{×}\text{1}\). By storing all values as matrices and using solvers based on matrix algebra, MATLAB programmers were able to achieve high efficiency, and hence low computational solving time.
In previous lessons, all the programs for the examples were written using scalar operations and variables. (Scalar means “one number”.) We now know that MATLAB has stored these scalar values as matrices for all required m-file operations. This lesson will discuss the use of matrices and matrix operations in MATLAB. If you are not comfortable with basic linear algebra concepts, see the Primer on Linear Algebra in Appendix A at the end of this textbook.
What is a matrix?
A matrix is a special organized way of representing groups of numbers. This organized form is similar to a grid or table, but where each cell, or “element”, has a standard reference. Matrices have two dimensions/directions called rows and columns. (Two dimensional matrices can be stacked to form three dimensional matrices, but we do not need to worry about this for now). In Figure 1, we see the standard notation for referencing an element in a matrix.
Figure 2 shows an example of how a matrix of numbers is often written on paper. In the bottom right of the figure we have noted the size of the matrix (the number of rows and columns). However, this is not mandatory or standard to write with each matrix explicitly.
Important Note: When reporting the
size of a matrix, the number of rows is followed by the number of
columns (e.g., \(\text{2×3}\) in Figure 2).
Do I need to know any special types of matrices?
Yes, there are several uses for a special type of matrix in linear
algebra. Examples include an identity matrix, a symmetric matrix, and an
upper-triangular matrix. MATLAB even has dedicated functions to create
some of these matrices. For example,
eye() creates an
identity matrix of any size you input. We will discuss these special
matrices more in Module 8.
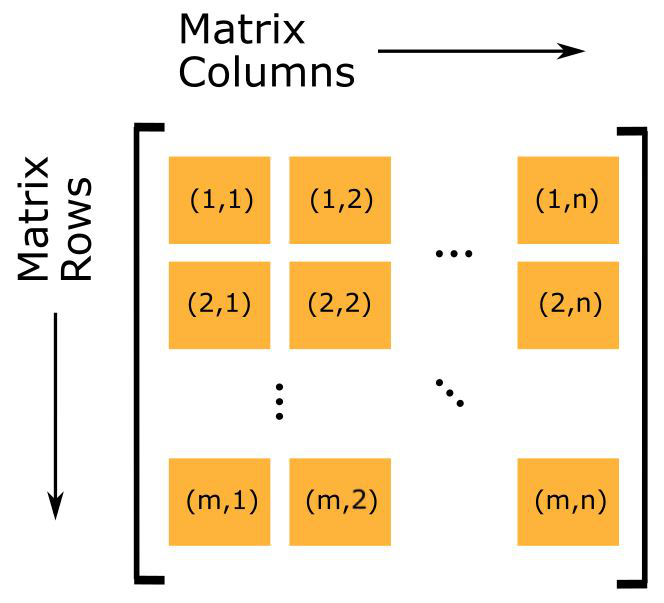
Figure 1: Generalized example of a matrix (size: \(\text{m} \times \text{n}\)).
\[\begin{bmatrix} \text{12} & \text{0} & \text{43} \\ \text{5} & \text{33} & \text{1.2} \\ \end{bmatrix}_{\text{2}\text{×}\text{3}}\]
Figure 2: A matrix with 2 rows and 3 columns (size:\(\ \text{2} \times \text{3}\)).
What is a vector?
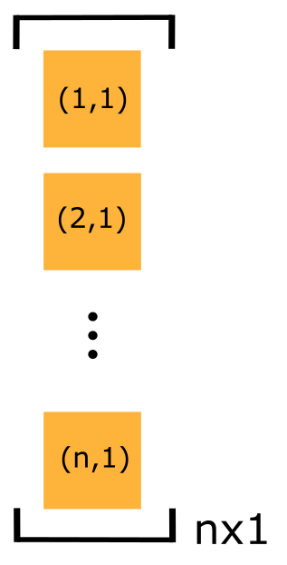
A vector is a category of matrices, a one-dimensional matrix. This means it has only one row (a row vector - see Figure 3) or one column (a column vector - see Figure 4). As mentioned before, the numbers to the bottom right of the vector denote the size of the vector.
Important Note: Since a vector is
just a type of matrix, the rules, notation, and syntax for matrices in
MATLAB also apply to vectors.
You can see an example of a vector containing numbers in Figure 5. Do not confuse programming (MATLAB) vectors with a general Euclidean vector, which has a magnitude and direction (e.g., 3 meters at 45 degrees). Also note that vectors and matrices are types of arrays. Arrays are the most general type of ordered data in programming.
 |
 |
|---|---|
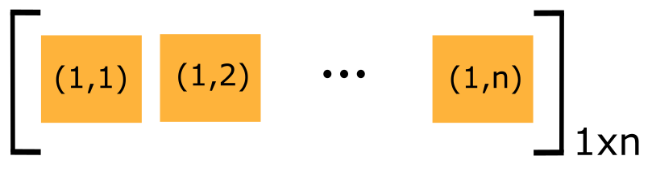| Figure 3: Generalized example of a row vector (size: \(1\times n\)). | Figure4: Generalized example of a column vector (size: \(n\times1\)). |
\[\begin{bmatrix} \text{4} & \text{10} & \text{99} \\ \end{bmatrix}\]
Figure 5: A vector with 1 row and 3 columns (size:\(\ \text{3×1}\)).
How do I define a vector or a matrix in MATLAB?
Matrices that contain all their elements in one row or all their elements in one column are called row and column vectors, respectively. If a matrix has more than one row and one column, it is a multidimensional matrix (the smallest size of a multidimensional matrix is \(\text{2×2}\)).
When defining a matrix in MATLAB, we must differentiate between rows and columns. To separate individual row elements, at least one space is required. To separate each matrix row, a semicolon is required. The nomenclature is the same for a matrix of any size.
The steps to input a matrix of any size are:
Define the matrix using a legal named variable.
Define the matrix by using a set of brackets [].
Inside the brackets, matrix rows are input with each element separated by at least one space.
Use a semicolon (;) to denote that the row input is complete.
Now, repeat steps 3 and 4, until all the rows are entered.
An example of how to enter a matrix is given next in Example 1.
Example 1
Input the following two matrices ([A] and [B]) into a MATLAB m-file.
\[\displaystyle\left\lbrack \text{A} \right\rbrack = \begin{bmatrix} \text{1} & \text{2} & \text{6} \\ \text{2} & \text{65} & \text{1} \\ \end{bmatrix} \text{ and } \left\lbrack \text{B} \right\rbrack = \begin{bmatrix} \text{2} & \text{3} \\ \text{2} & \text{1} \\ \text{9} & \text{3} \\ \end{bmatrix}\]
Solution
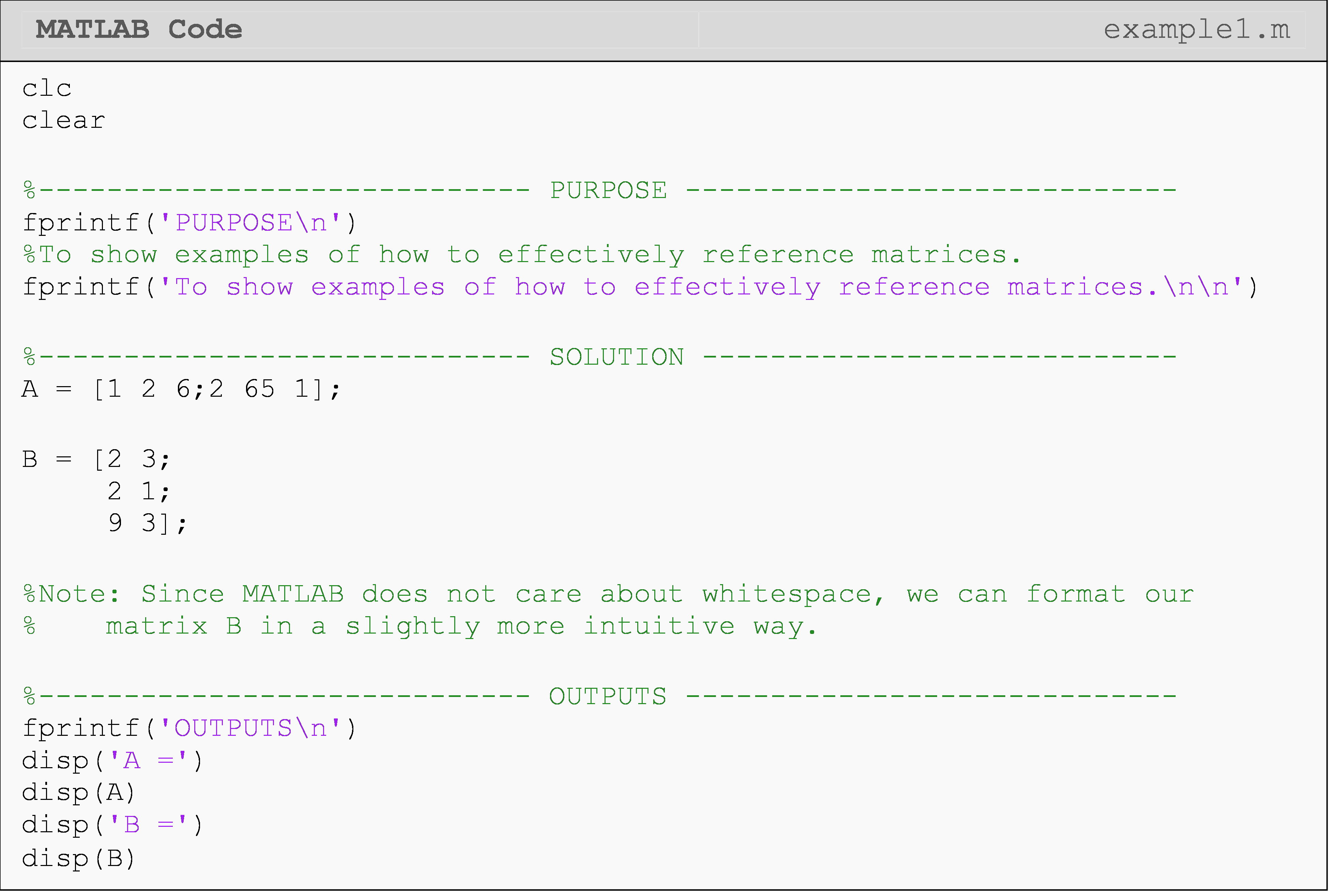
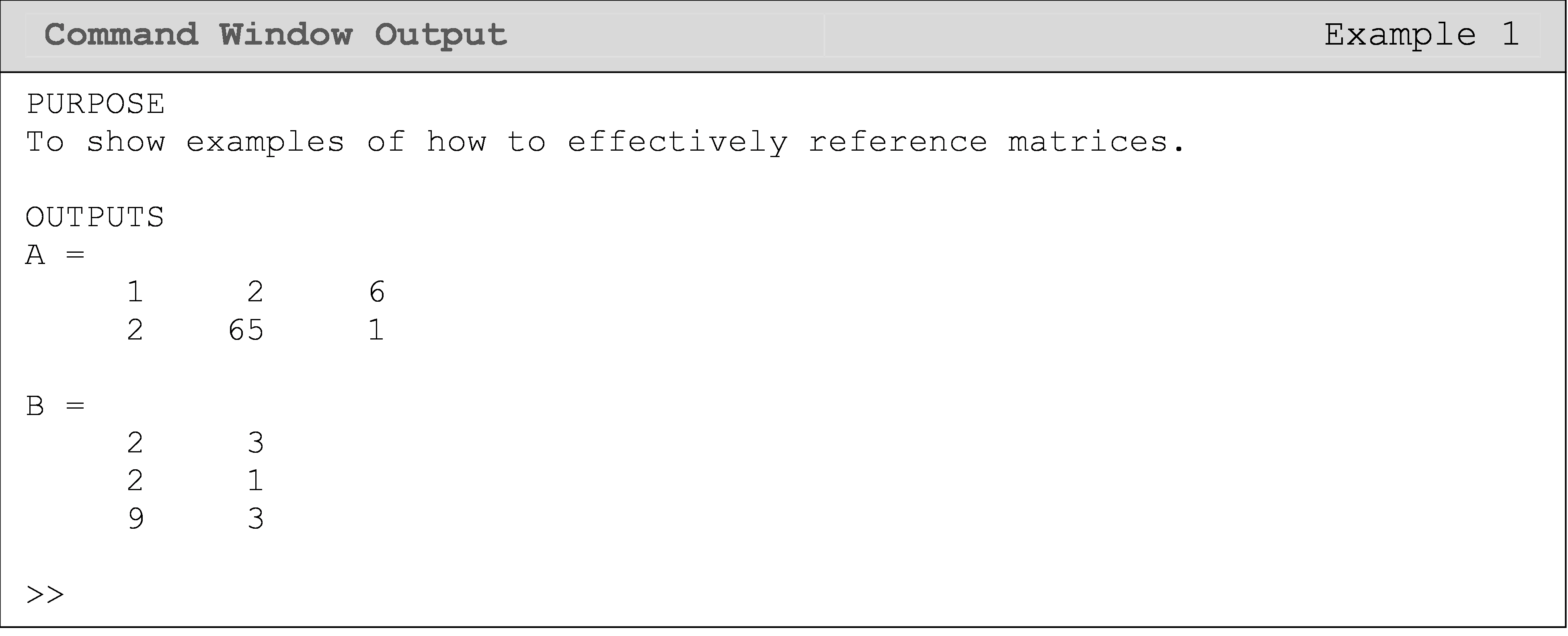
You can see the steps for inputting a matrix being followed in Figure 1. Note the differences between inputting a scalar and a matrix.
What are some basic functions and commands for matrix manipulation?
MATLAB has implemented many built-in functions that make basic matrix manipulations simpler and these are shown in Table 1.
Table 1: Several commonly used matrix commands and operators. The input to the listed commands is the matrix [A] and [B] (where applicable).
| Task | Syntax | Explanation |
|---|---|---|
| Isolating a matrix element | A(r#,c#) |
Calls a matrix element by a row # and column # |
| Maximum dimension of a matrix/vector | length(A) |
Outputs the largest dimension of a vector/matrix |
| Size of a matrix | size(A) |
Has two outputs: the number of rows and the number of columns of a matrix. |
| Last element of a dimension | A(end,1) |
References/indexes the last element in that dimension. |
| Matrix referencing shorthand | A(:,1) |
Yields the entire first column. The “:” references “all of that dimension”. |
| Matrix referencing shorthand | A(1:20,1) |
Yields rows 1 through 20 in column 1 of matrix [A]. |
| Develop a zero matrix | zeros(m,n) |
Outputs a matrix of size \(\text{m}\times\text{n}\) with all zeros elements |
| Create an identity matrix | eye(n) |
Outputs an identity matrix of size \(\text{n}\times\text{n}\) |
| Develop a ones matrix | ones(m,n) |
Outputs a matrix of size \(\text{m}\times\text{n}\) with all elements equal to one |
| Create an arbitrary square matrix | magic(n) |
Outputs an arbitrary square matrix of size \(\text{n}\times\text{n}\) |
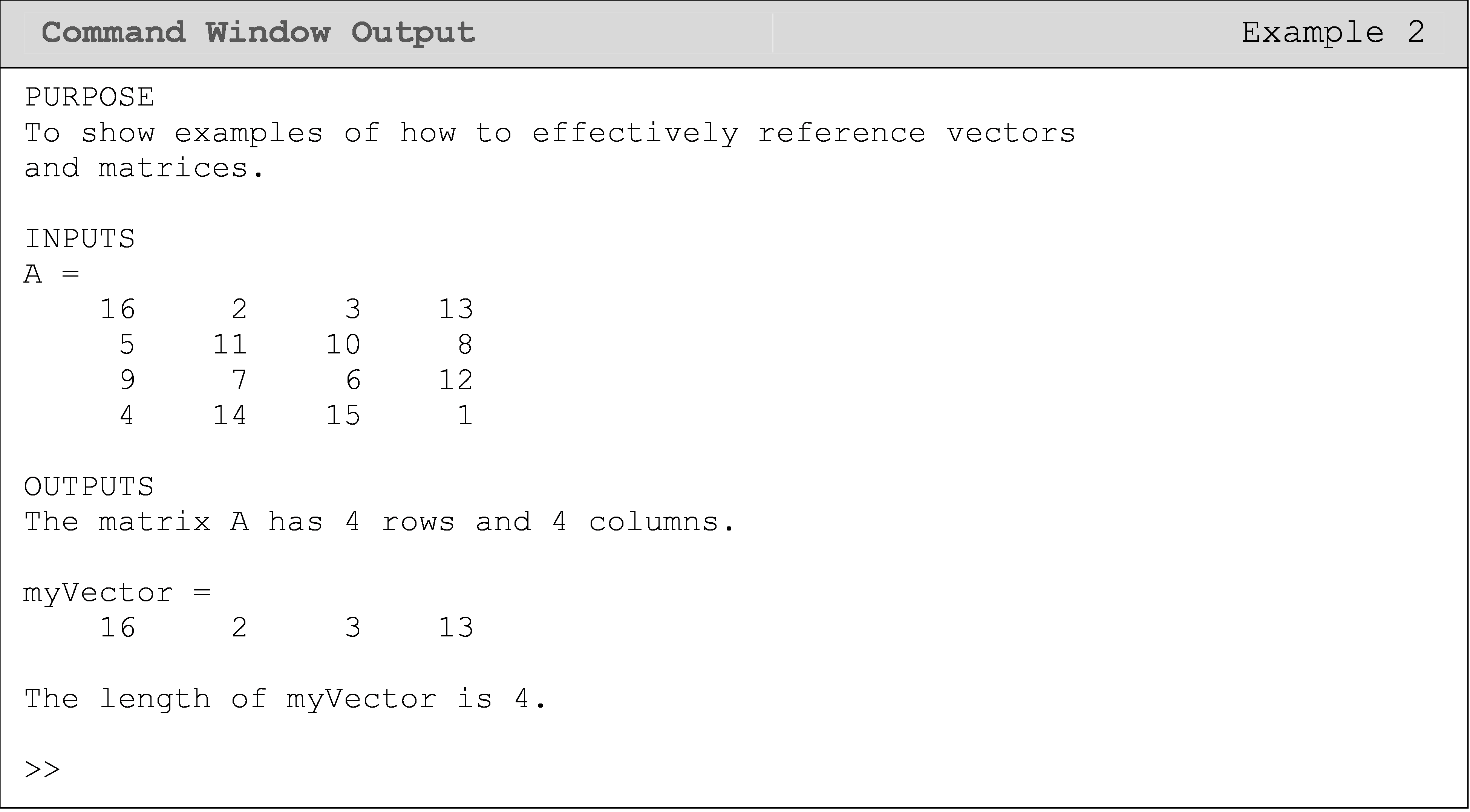
Example 2
Create an arbitrary matrix, and find its dimensions. Then create a vector from a subset of this matrix and calculate the number of elements in it.
Solution
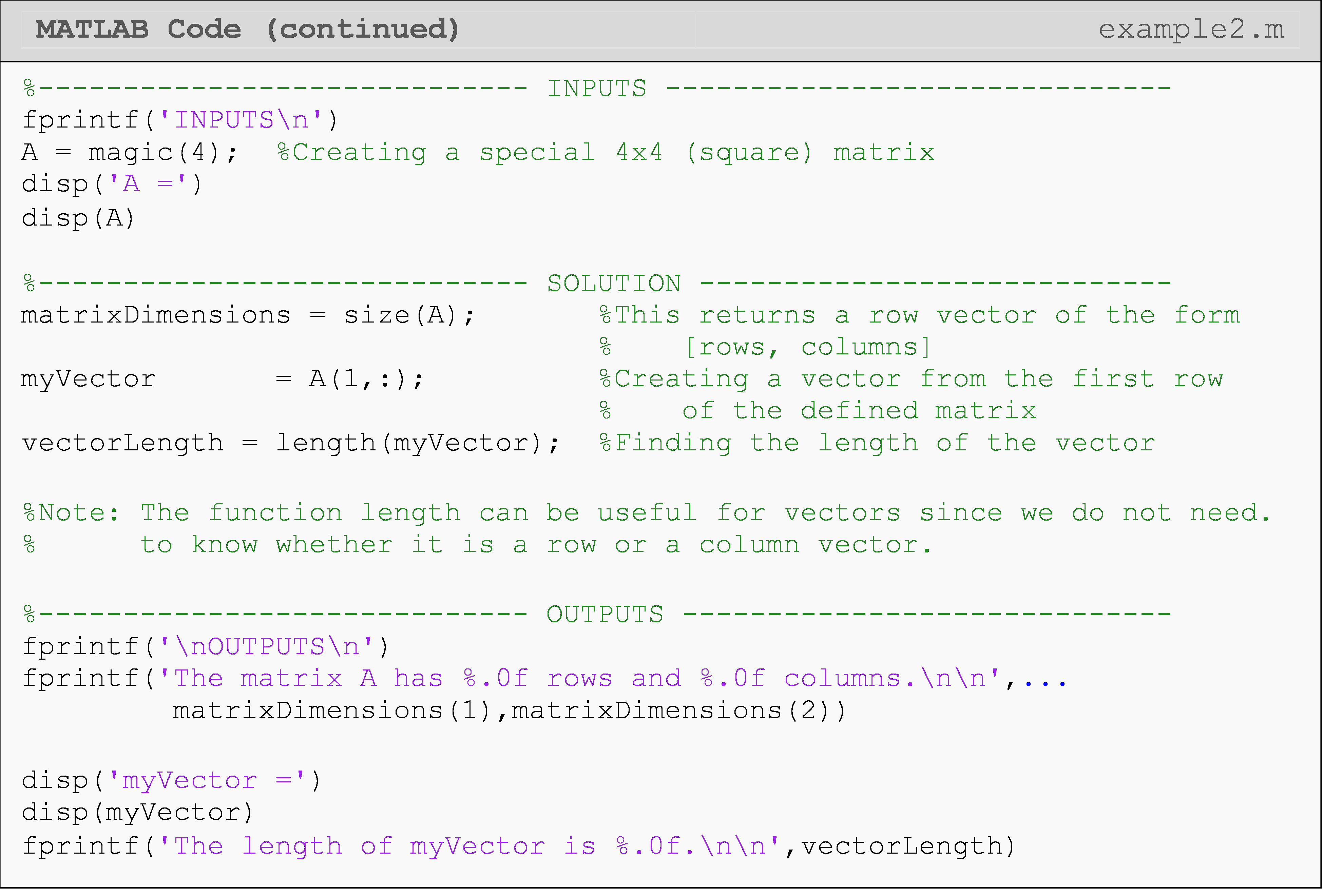
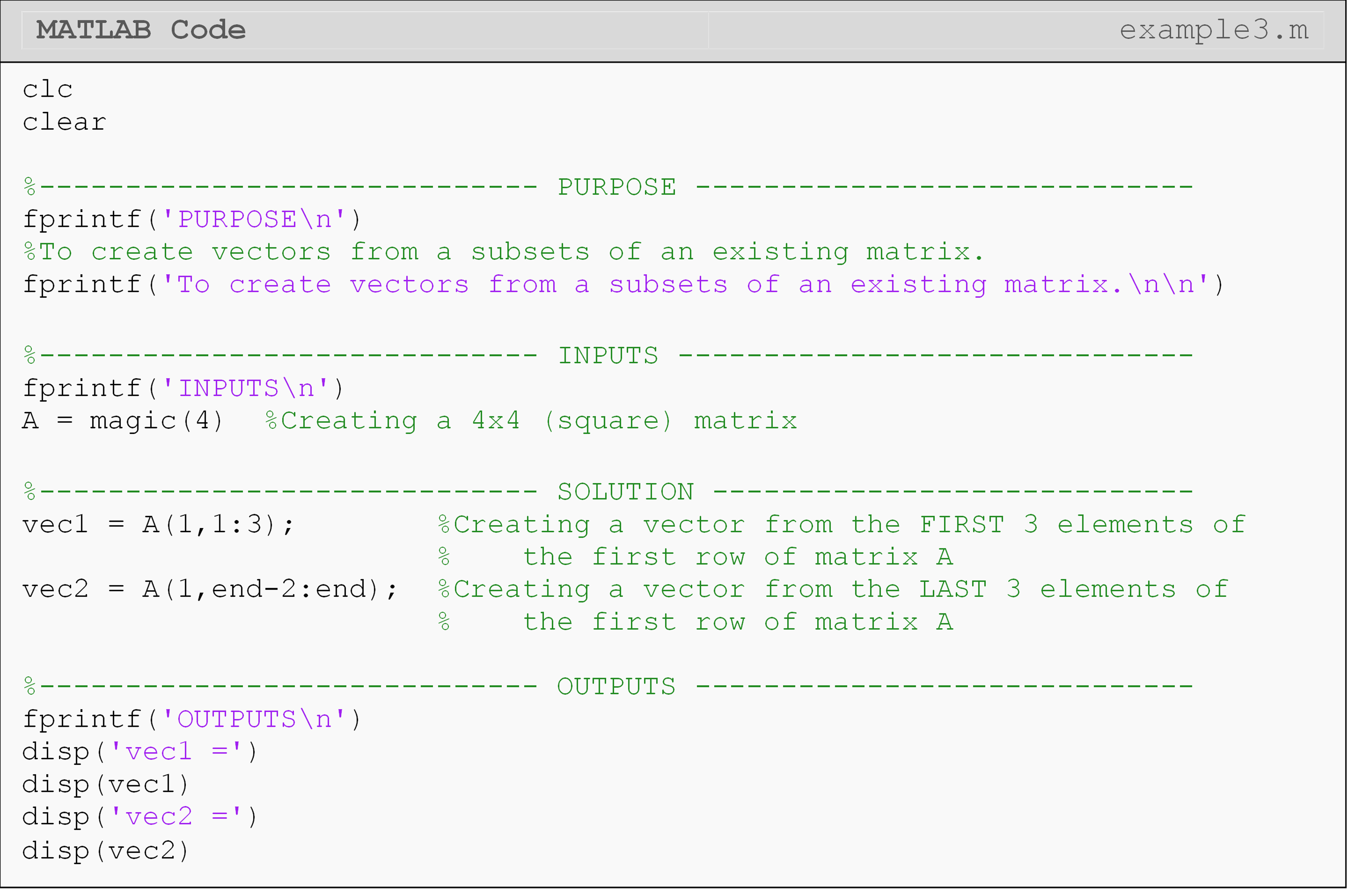
Example 3
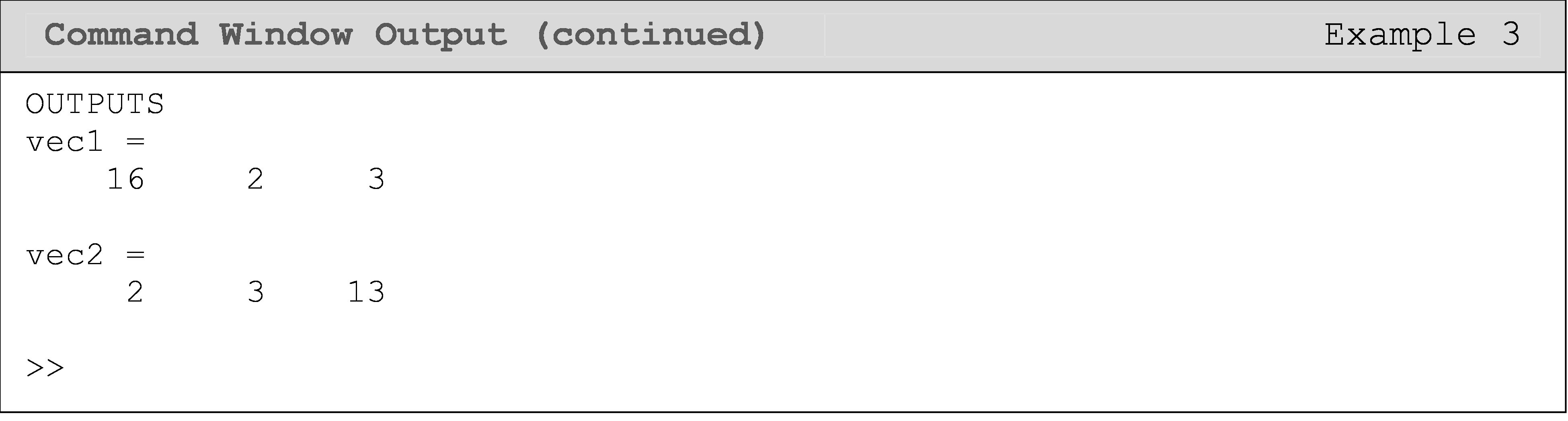
Create an arbitrary matrix \([A]\). Then create two vectors, vec1 and
vec2, from subsets of that matrix.
The vector, vec1, should contain the first three elements of the
first row of the matrix \([A]\). The vector, vec2, should contain the
last three elements of the first row of the matrix \([A]\).
Solution
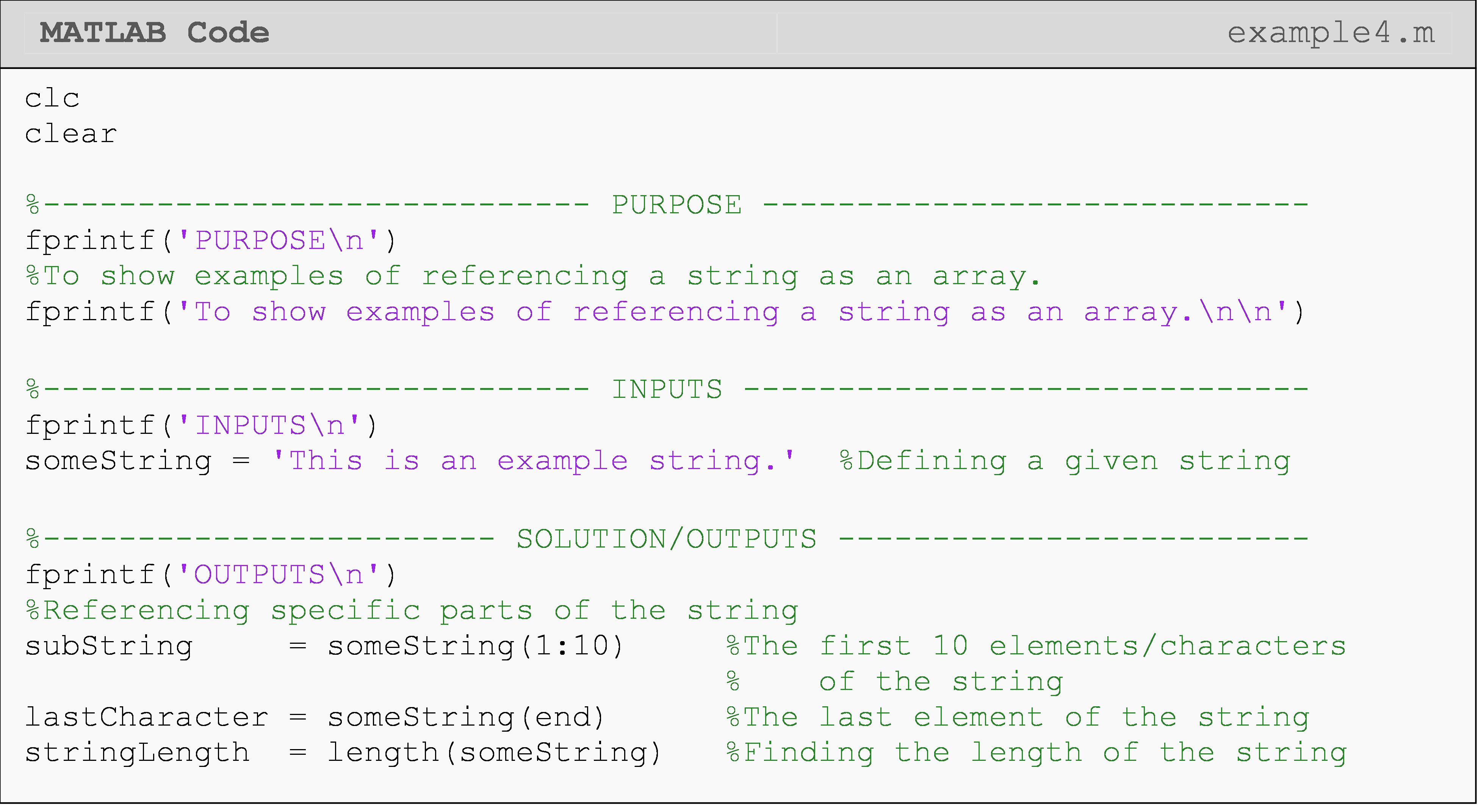
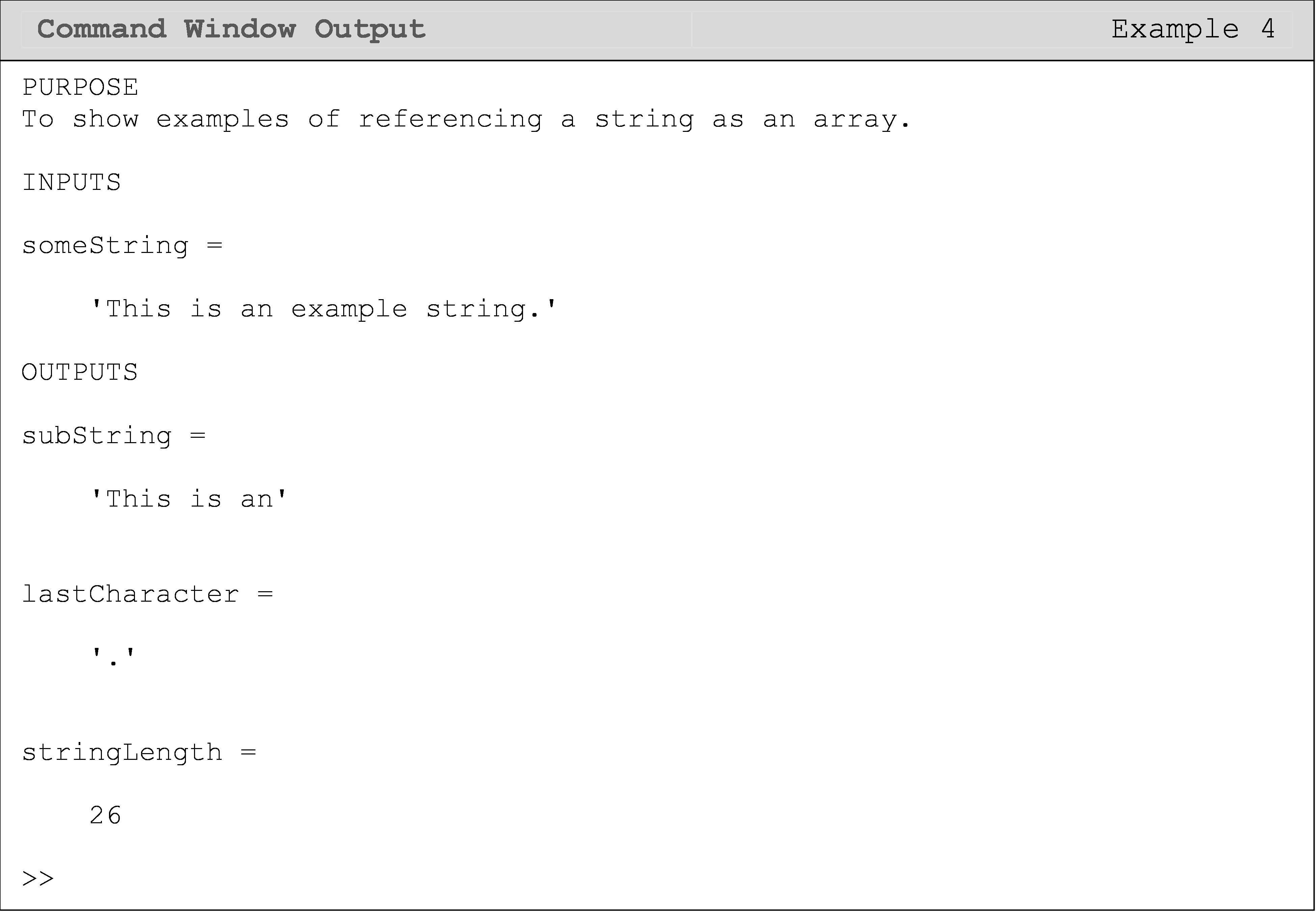
How can I reference strings as vectors?
In Lesson 2.2, we discussed characters and strings. In MATLAB and many other programming languages, strings (or arrays) of characters, can be referenced the same way as a vector. See Example 4 for usage. This can be especially useful if we only want to look at a particular part of a string/text.
Lesson Summary of New Syntax and Programming Tools
| Task | Syntax | Example Usage |
| Isolating a matrix element | A() |
A(r#,c#) |
| Maximum dimension of a matrix/vector | length() |
length(A) |
| Size of a matrix | size() |
size(A) |
| Last element of a dimension | end |
A(end,1) |
| Matrix referencing shorthand (whole dimension) | : |
A(:,1) |
| Matrix referencing shorthand (partial dimension) | a:b |
A(1:20,1) |
| Develop a zero matrix | zeros() |
zeros(m,n) |
| Create an identity matrix | eye() |
eye(n) |
| Develop a ones matrix | ones() |
ones(m,n) |
| Create an arbitrary square matrix | magic() |
magic(n) |
Multiple Choice Quiz
(1). The MATLAB function that outputs the number of rows and columns of a matrix is
(a) dimensions()
(b) mdim()
(c) msize()
(d) size()
(2). When inputting a matrix, each new row is separated by a
(a) :
(b) ;
(c) |
(d) ,
(3). What is the output of the last line?
(a) -6
(b) 3
(c) 4
(d) 12
(4). Given a matrix,[A], which of the following will return the element from the second row and third column?
(a) A(3)(2)
(b) A(3,2)
(c) A(2)(3)
(d) A(2,3)
(5). What is the Command Window output of the following program?
(a) ans = 64
(b) ans = 48
(c) ans = 40
(d) ans = 30
Problem Set
(1). Create a row and column vector each with five elements and store each of them in a variable. Then find the size and length of each vector.
(2). Create a \(\text{3} \times \text{4}\) matrix and store it in a
variable. Find its size and display the number of rows and the
number of columns with a single fprintf() function.
(3). Create a \(\text{4} \times \text{4}\) matrix and store it in a variable. Then find and display the product of the elements at the fourth row, second column and the second row, third column.
(4). Create an \(\text{n} \times \text{n}\) matrix and store it in a variable. Then create a column vector from the first column of that matrix and store it in a variable. Remember not to hardcode! Your solution should work for any size matrix.
(5). Create an \(\text{m} \times \text{n}\) matrix, where \(\text{m} > \text{n} > \text{3}\) and store it in a variable. Then create a row vector from the last three elements of the first row of the matrix.