Module 4: MATH AND DATA ANALYSIS
Learning Objectives
After reading this lesson, you should be able to:
find the derivatives of continuous functions,
find the derivatives of discrete functions,
use derivatives to solve basic engineering problems.
What is a derivative?
The derivative of a function represents the rate of change of a variable with respect to another variable (see Figure 1).
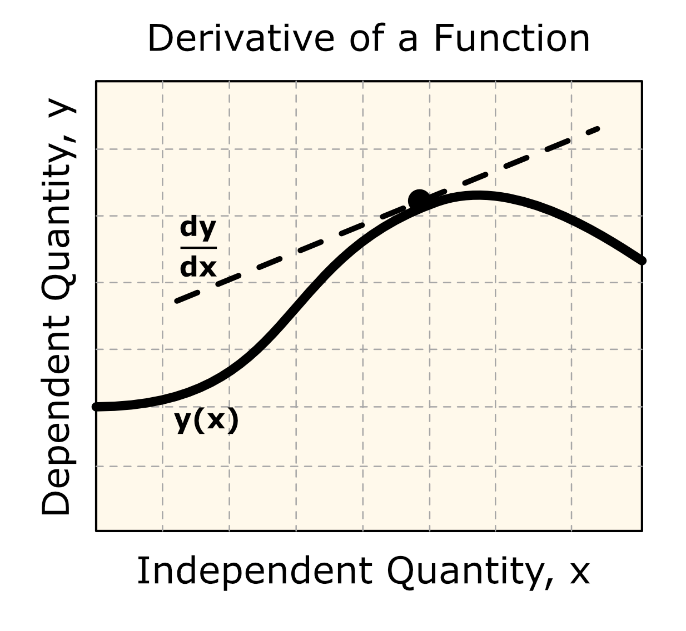
Figure 1: Shown is a line tangent to a function, y(x).
For example, the velocity of a body is defined as the rate of change of the location of the body with respect to time. The location is the dependent variable while time is the independent variable. Now if we measure the rate of change of velocity with respect to time, we get the acceleration of the body. In this case, the velocity is the dependent variable while time is the independent variable.
Recall from calculus, the derivative of a function \(f(x)\) is defined as
\[f^{'}(x) = \lim_{\Delta x \rightarrow 0}\frac{f(x + \Delta x) - f(x)}{\Delta x}\]
The value of the first derivative of a function evaluated at a point on the function is the slope of the line tangent to the function at that point. This concept is depicted in Figure 1.
How do I take the derivative of a function in MATLAB?
To do the differentiation, one needs three inputs:
The function f(x) that needs to be differentiated.
The variable with respect to which the function needs to be differentiated, x.
The order of derivative needed, n.
In MATLAB, these three inputs are required to find the derivative of a
symbolic function. To differentiate a symbolic function, the MATLAB
function diff() can be used. The order of the derivative can be
specified, as shown in Example 1, but the diff() function defaults to
a first-order derivative if no order is given.
It is important to note that the diff() function is also used to find
the difference between corresponding points in two vectors (covered in
more detail later in this lesson), and if the programmer does not use
the correct input variable placement (syntax), the output would be
incorrect. Example 1 shows the diff function being used to find a
derivative.
Example 1
Using the diff() function, write a program that finds and outputs the
following.
(a) \(\displaystyle\frac{d}{dx}\left( 7e^{3x} \right)\)
(b) \(\displaystyle\frac{d^{2}}{dx^{2}}\left( \sin(x^{2}) + x^{6} \right)\)
Solution

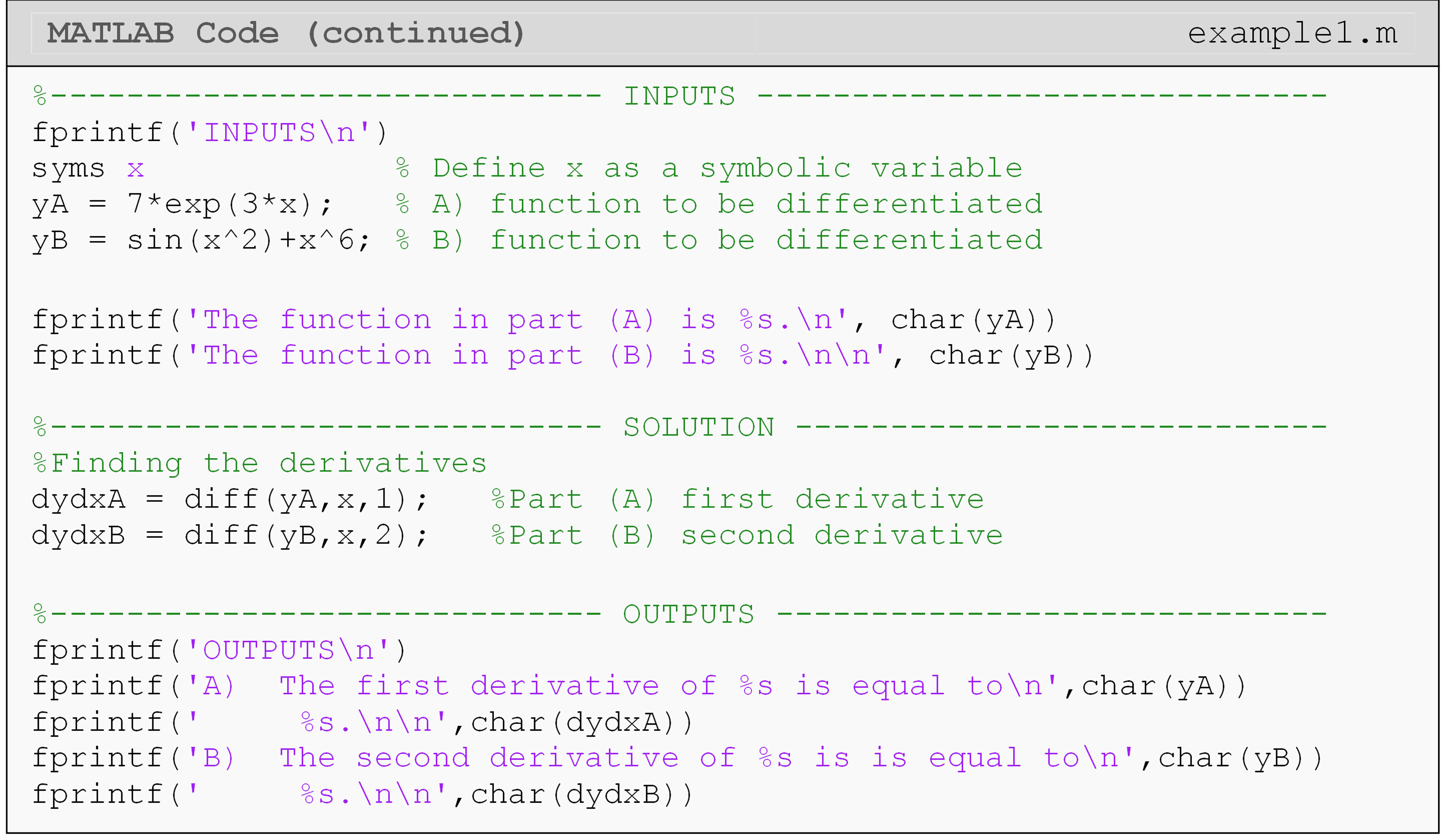
To solve the problem given in Example 3 one must first enter the
symbolic functions to be differentiated. The syms command must then be
used to define the symbolic variable(s) before defining any
function(s).

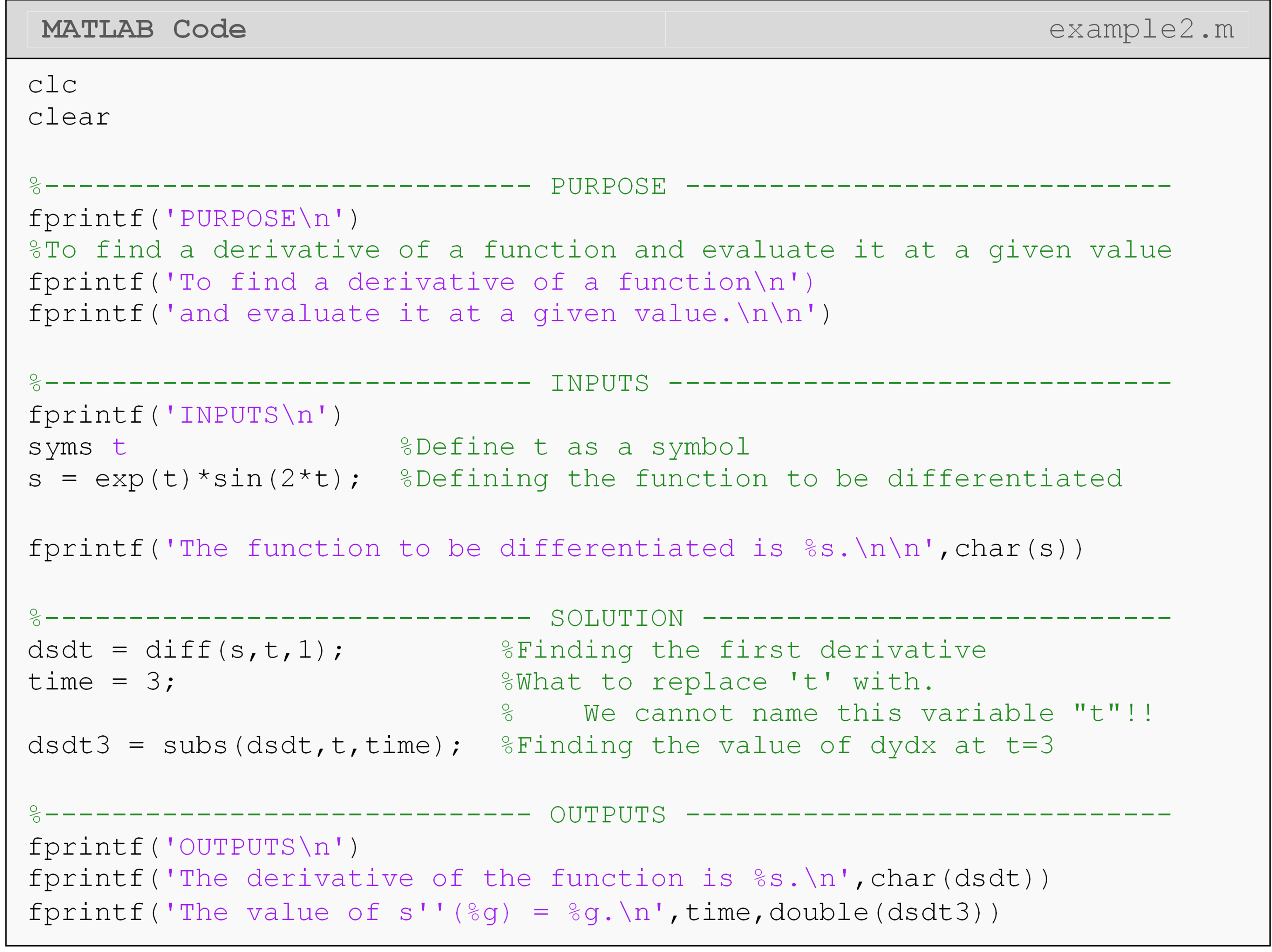
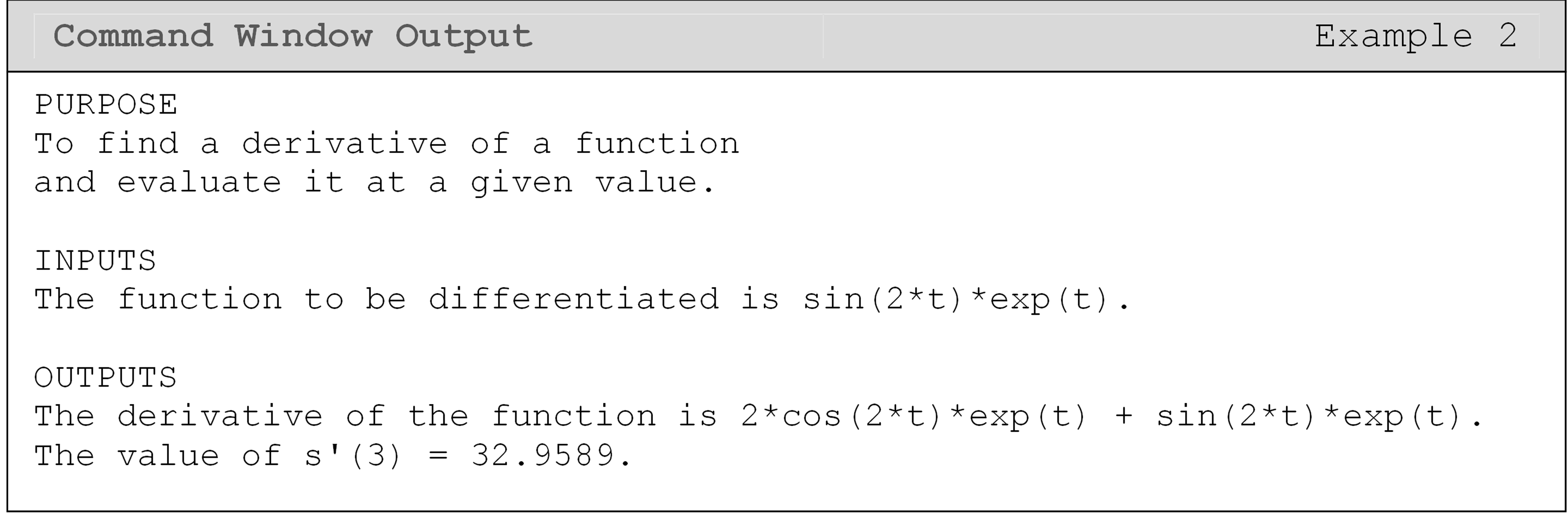
Example 2
Find the slope of the tangent line to the function\(s(t) = e^{t}\sin(2t)\)
at \(t = 3\), using the diff() and subs() functions.
Solution
The diff() function is used to find the slope of the tangent line
(first derivative) and then the subs() function is called to evaluate
the slope of the tangent line at the specified value of t. To show the
inputs and outputs for this example, the char() function is used to
convert symbolic expressions into printable strings.
Where are derivatives used in engineering?
Derivatives have many uses in engineering and mathematics. Some derivatives are easy to find, others are complex, and some are even partial.
Derivatives are used to set up differential equations, which will be covered in Lesson 4.9. In engineering and physics, one of the most common uses of derivatives is in the relationship of position, velocity, and acceleration functions of a body. Where given the position of a body as a function of time, the derivative of position with respect to time is the velocity function. The derivative of velocity with respect to time is the acceleration function of the body.
Another common use of derivatives is finding the location of minimum and maximum points of a function. We know that the value of the derivative is the slope of the line tangent to a function at a given point. If we set the found derivative equal to zero (tangent slope is zero) and solve for the independent variable, we can find the local minima or maxima of a function. This technique is used for optimization.
Example 3
The position of a body is defined by the function s(t) as
\[s(t) = 7t^{3} + \ln(2t) - 9.8t^{2}\]
where t is in seconds, and s is in m/s. Using MATLAB, output the velocity and acceleration functions of the body. Also, find the velocity and acceleration of the body at \(t = 2.5\) seconds.
Solution
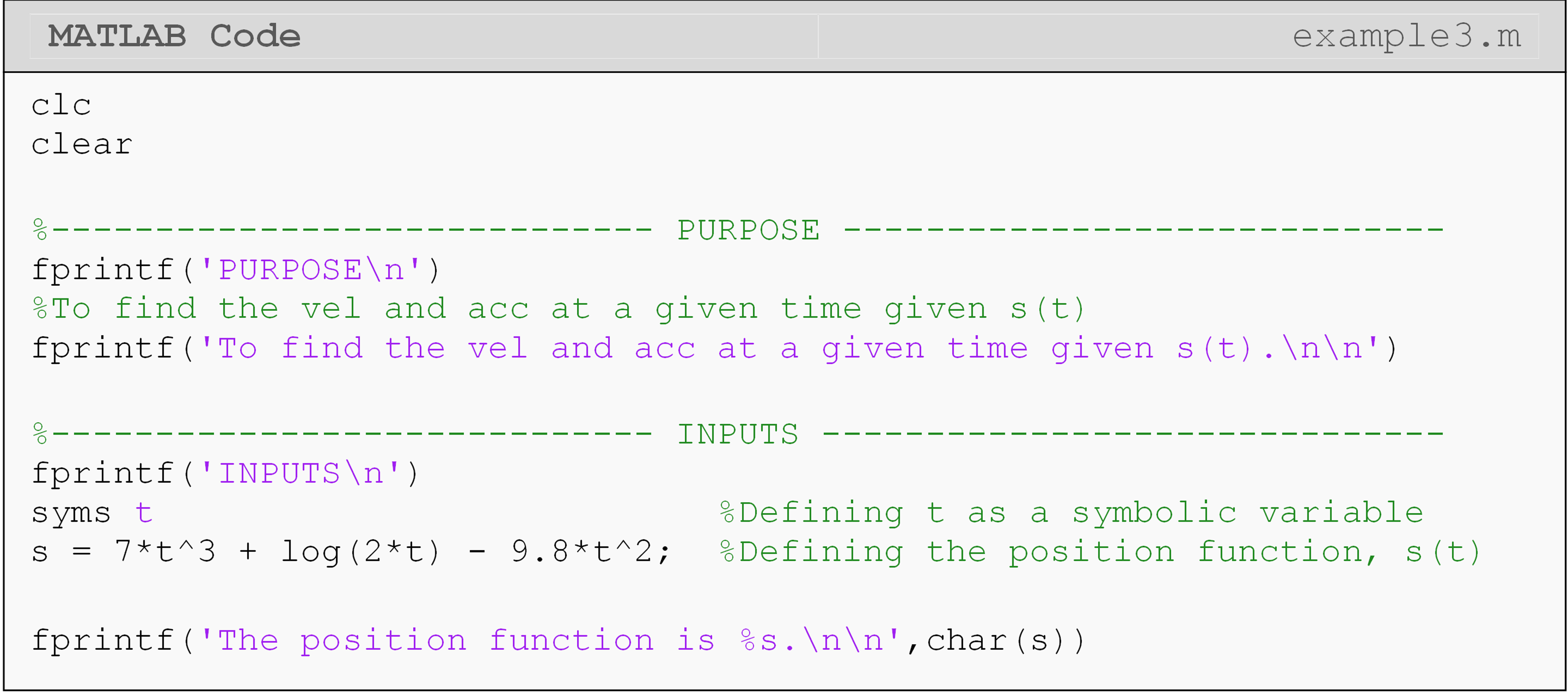
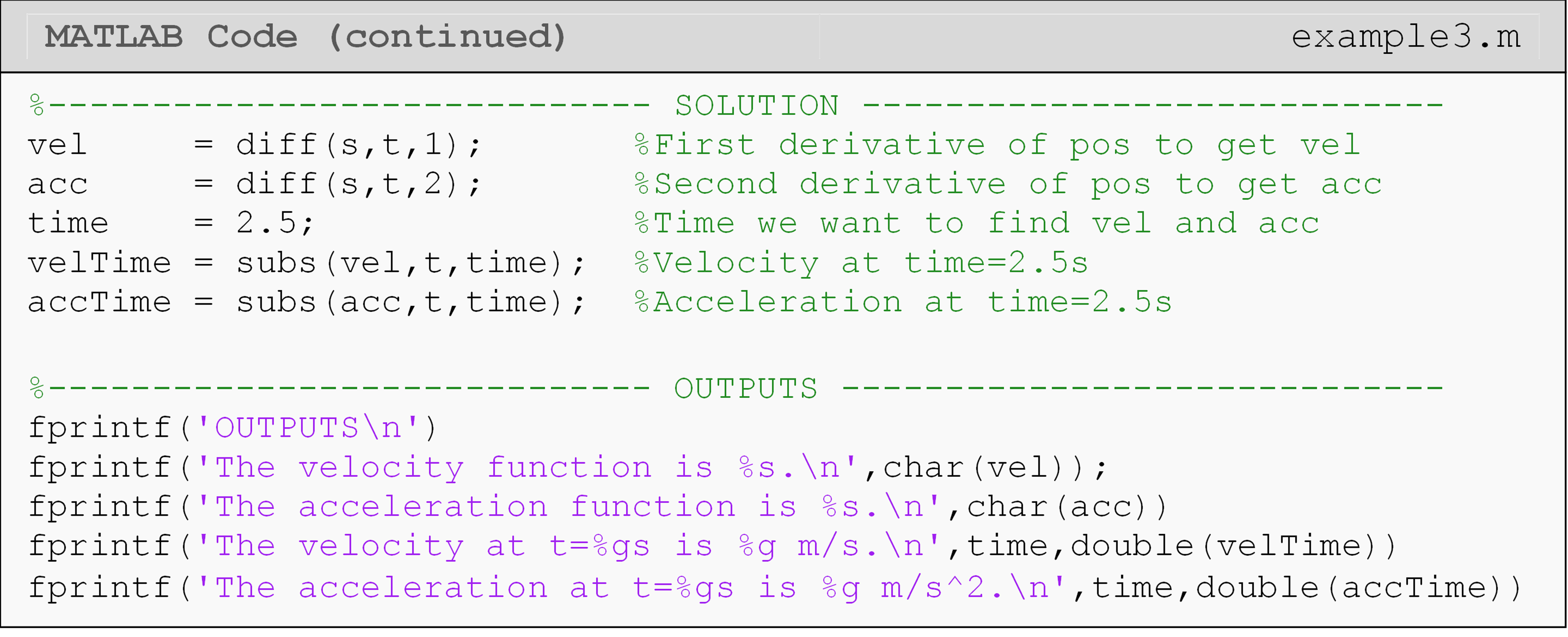
In Example 3, the diff() function is used to find the velocity and the
acceleration of the body. The subs() function is then used to find the
velocity of the rocket at \(t = 2.5\) seconds.

How do I find the derivative of a discrete function in MATLAB?
The diff()
function can also be used in the case of taking the derivative of a
function with discrete data points. That is, differentiating a matrix or
vector containing independent variables such as
\(\left\lbrack \begin{matrix}2 & 4 & 6 & 8\end{matrix} \right\rbrack\).
If a continuous/exact mathematical function is not available and a
discrete data set is presented (e.g., position sensor reading), the
diff() function
can be used to find the differences, or steps, between subsequent data
entries which in turn can be used to find the numerical derivative.
The following examples show this discrete/numerical differentiation
performed with the
diff() function.
The difference between subsequent vector elements is used to find the
numerical derivative. This approximation is generally referred to as the
finite difference
formula.
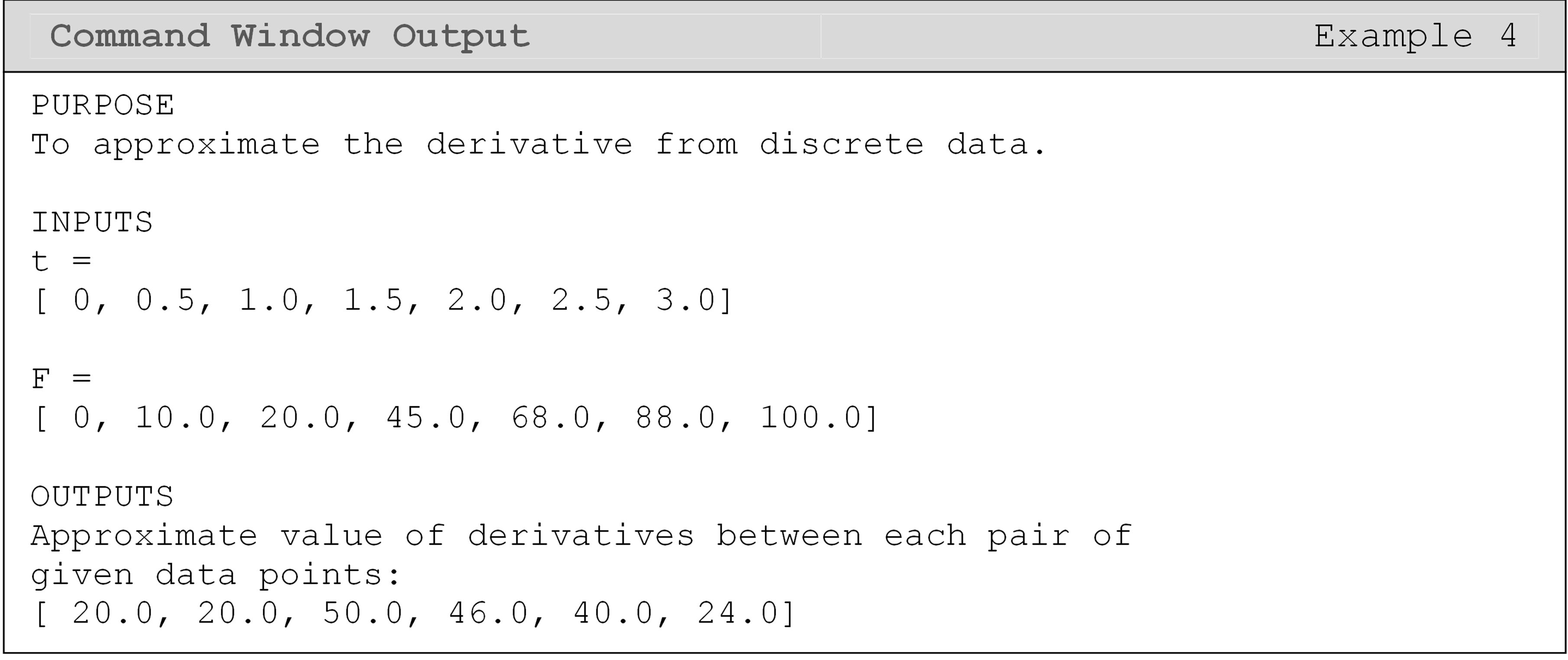
Example 4
Find the approximate derivative of the discrete function, F(t), given the following points.
The discrete function F(t) is given by
| t | 0.0 | 0.5 | 1.0 | 1.2 | 2.0 | 2.5 | 3.0 |
| F | 0.0 | 10 | 20 | 45 | 68 | 88 | 100 |
Use the forward divided difference method as the numerical algorithm to estimate the first derivative between the discrete data points.
The forward divided difference formula is given by \(\displaystyle\frac{\text{d}\text{F}\text{(}\text{t}\text{)}}{\text{dt}} \approx \displaystyle\frac{\text{F}\left( \text{t} + \Delta\text{t} \right) - \text{f}\text{(}\text{t}\text{)}}{\Delta\text{t}}\).
Solution
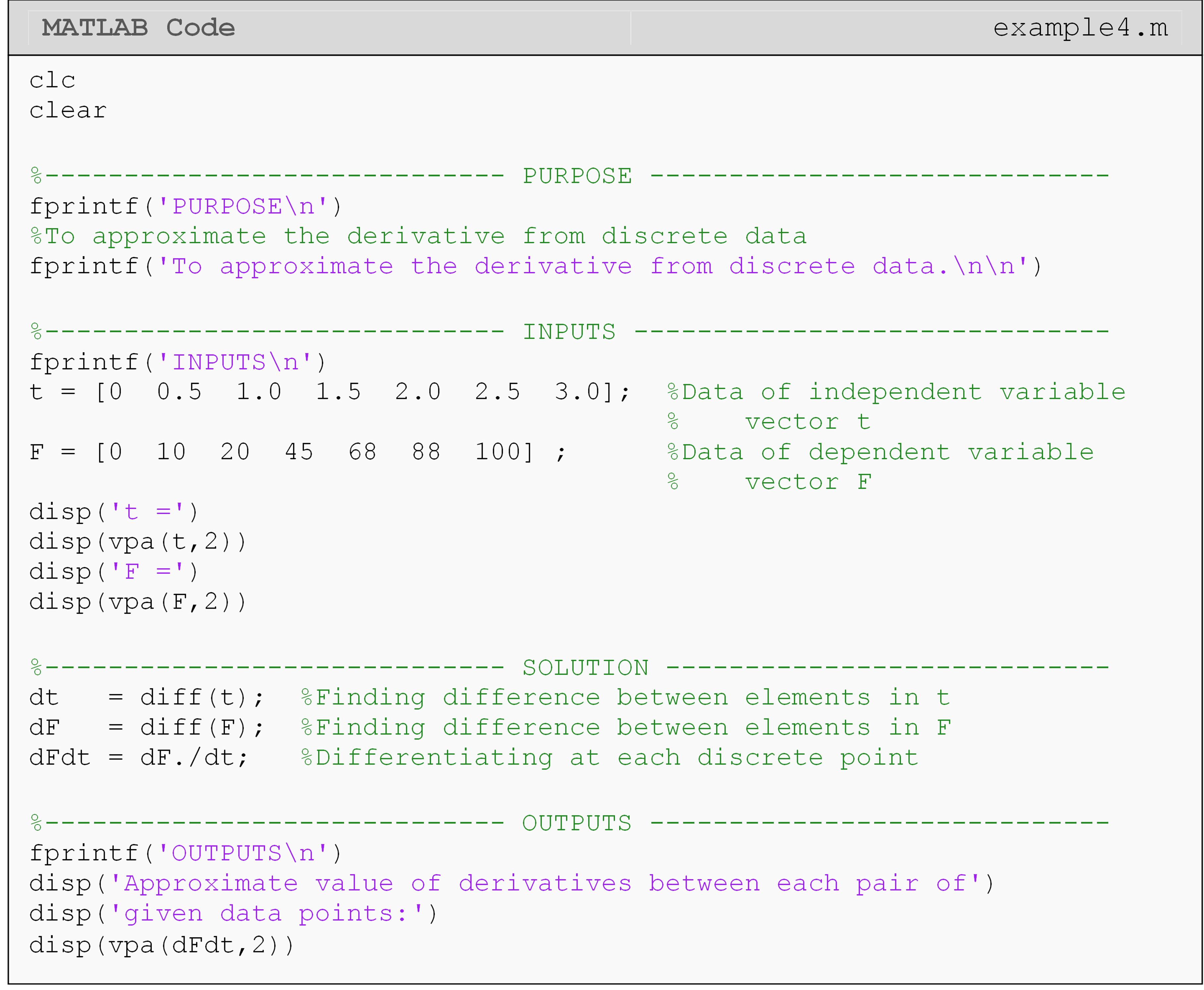
Note, the period (.) in dF./dt acts as an element-by-element array operator. This is fully covered in Lesson 4.6 on Linear Algebra, which you can review as needed.
Note that other numerical differentiation algorithms are possible and should be considered depending on the particular discrete data set and application. In general, as the data sample resolution and sampling rate increases, the differences between the values obtained using numerical differentiation methods becomes negligible.
Lesson Summary of New Syntax and Programming Tools
| Task | Syntax | Example Usage |
|---|---|---|
| Find the derivative of a symbolic function | diff() |
diff(func,x,2) |
| Find the difference between adjacent elements in a vector | diff() |
diff(xPoints) |
Multiple Choice Quiz
(1). The MATLAB function for symbolic differentiation is
(a) dif()
(b) diff()
(c) int()
(d) differentiate()
(2). To find \(\displaystyle\frac{d^2}{dx^2}\left(7e^{4x}\right)\), the correct line of code to add to the following program is

(a) diff(7*exp(4*x),x,2)
(b) diff(7*exp(4*x),x,1)
(c) diff(7exp(4*x),x,1)
(d) diff(7*exp^(4*x),x,2)
(3). To find \(f(3)\), given \(f(x)=x^2+8\), the correct line of code to add to the following program is

(a) subs(f,3,x)
(b) subs(f,x,3)
(c) f(3)
(d) function(f,3)
(4). The diff() function is used to
(a) find the derivative of a symbolic function.
(b) calculate the difference between adjacent elements in a vector.
(c) perform the subtraction of two variables.
(d) both A and B
(5). Given the discrete function, y(x), as the vectors x and y of discrete data points, which of the following would not appear in a program that approximates the first derivative between data pairs?
The following partial program is provided for reference.

(a) diff(y,x,1)
(b) diff(x)
(c) diff(y)
(d) diff(y)./diff(x)
Problem Set
(1). Use the diff() function to find
\(\displaystyle\frac{d}{dx}(7\sin(4x))\) at x = 3.5
(2). Use the diff() function to find
\(\frac{d^{2}}{dx^{2}}\left( 4\sin(4x^{2}) + e^{x} \right)\) at x = 3.75
(3). A rectangle is inscribed in a semi-circle of radius 2m (as shown in Figure A). If the area of the rectangle is to be maximized, find the dimensions of the rectangle.
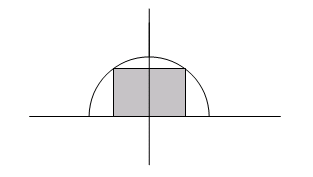
Figure A: Rectangle inscribed inside circle used for Exercise 3.
(4). The velocity of a rocket is given by
\[\nu(t) = 2000\ln\left\lbrack \frac{14 \times 10^{4}}{14 \times 10^{4} - 2100t} \right\rbrack - 9.8t,\ 0 \leq t \leq 30\]
where \(\nu\) is given in m/s and \(t\) is given in seconds. At \(t = 16s\), find the velocity and acceleration of the rocket. Display your results in the command window using the appropriate method.
(5). An experimental single-piston pump is put through a series of tests in a laboratory. The velocity (as a function of time) of the piston in the pump is measured as various forces are applied to the piston. To determine expected bearing life, rod stress, and pumping capacities, the piston force function (as a function of time) must be found. To help determine the efficiency of the pump, the kinetic energy function of the piston must also be determined (assume the piston has no potential or rotational stored energy).
The piston velocity function is
\[v(t) = (3.21)\sin(2.3t) + \cos(2.3t)\ln(5.2t)\text{\ ,\ \ \ }\ \ \ 0 < t \leq 10\]
where,
v is the velocity given in meters/second
t is the time given in seconds
Given is the mass of the piston as 0.73 kg. Using MATLAB, write a program that outputs:
the piston force function,\(F(t)\),
the piston kinetic energy function, \(KE(t)\),
the maximum piston speed, m/s,
the minimum piston speed, m/s.
Hint:
\[\text{Force} = \text{mass} \times \text{acceleration}\]
\[\text{Kinetic Energy} = \frac{1}{2} \times \text{mass} \times \text{velocity}^{2}\]
(6). There is strong evidence that the first level of processing of what we see is done in the retina. It involves detecting something called edges or positions of transitions from dark to bright or bright to dark points in images. These points usually coincide with boundaries of objects. To model the edges, derivatives of functions such as
\[f(x) = \left\{ \begin{matrix} 1 - e^{- ax},\begin{matrix} & x \geq 0 \\ \end{matrix} \\ e^{ax} - 1,\begin{matrix} & \text{ }x \leq 0 \\ \end{matrix} \\ \end{matrix} \right.\ \]
need to be found. Find \(f'(0.1)\) and \(f'( - 0.1)\). Assume \(a = 0.24\).