Module 7: FUNCTIONS
Learning Objectives
After reading this lesson, you should be able to:
add descriptions of your function for the help command,
define your own custom errors and warnings in a function.
How can I add a description for my function?
Remember the
help command we
learned about at the beginning of this course? This utility function
also allows us to get a summary of information about any of our custom
functions. MATLAB allows us to provide helper
descriptions
in the functions that we write so that we can reference back to them
through the Command Window if needed. These function descriptions come
in handy when trying to quickly remember what a function does and how to
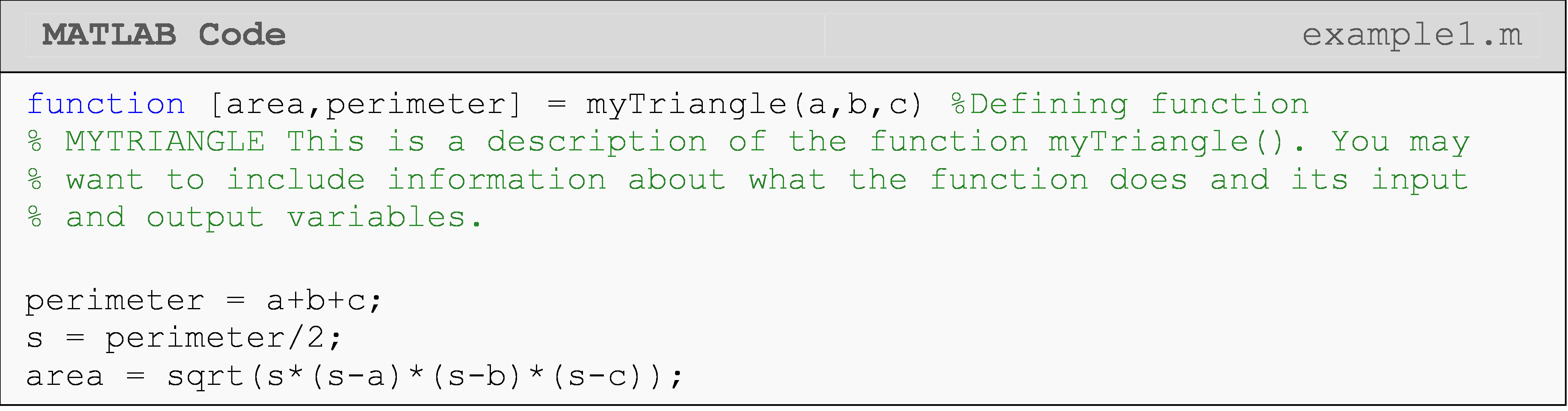
use it. The spacing and formatting of the description seen in Example 1
is optional but suggested for clarity. You can also include a brief
function usage example within the function description!
The help text must come immediately after the function definition line.
This is the only rule. However, it is standard to make the first word in
the help description as the function name in all capital letters. This
will make any other mentions of the function name bolded in the help
text (see Command Window output for Example 1). In Example 1, the
function is myTriangle(), so the first word of the second line is
"MYTRIANGLE".
How can I define errors and warnings inside my function?
We first learned about defining custom warning and error messages in
Lesson 6.3: Writing Better Code (as well as many other helpful tips).
Now, we will apply the
error()
and
warning()
functions inside a custom function that we write. The main difference
for error handling in our custom functions is that you will need to
foresee possible mistakes or misunderstandings that users might have.
This can include mistakes a user might make regarding general
information like mathematics or domain/problem-specific knowledge. For
example, if you know that it is not possible to have a negative measure
of length, you may want to check that the length input to your function
is not a negative number and display a warning message if the length
given is less than zero. As a side note,
error()
and
warning()
functions are not exclusive to our custom functions but can be
implemented anywhere in your MATLAB code.
As seen in Example 2, if the user triggers a
warning(), a
custom message will be displayed, and the running program will continue
to execute. However, if the user triggers an
error(),
the program will halt, and the error message will be displayed.
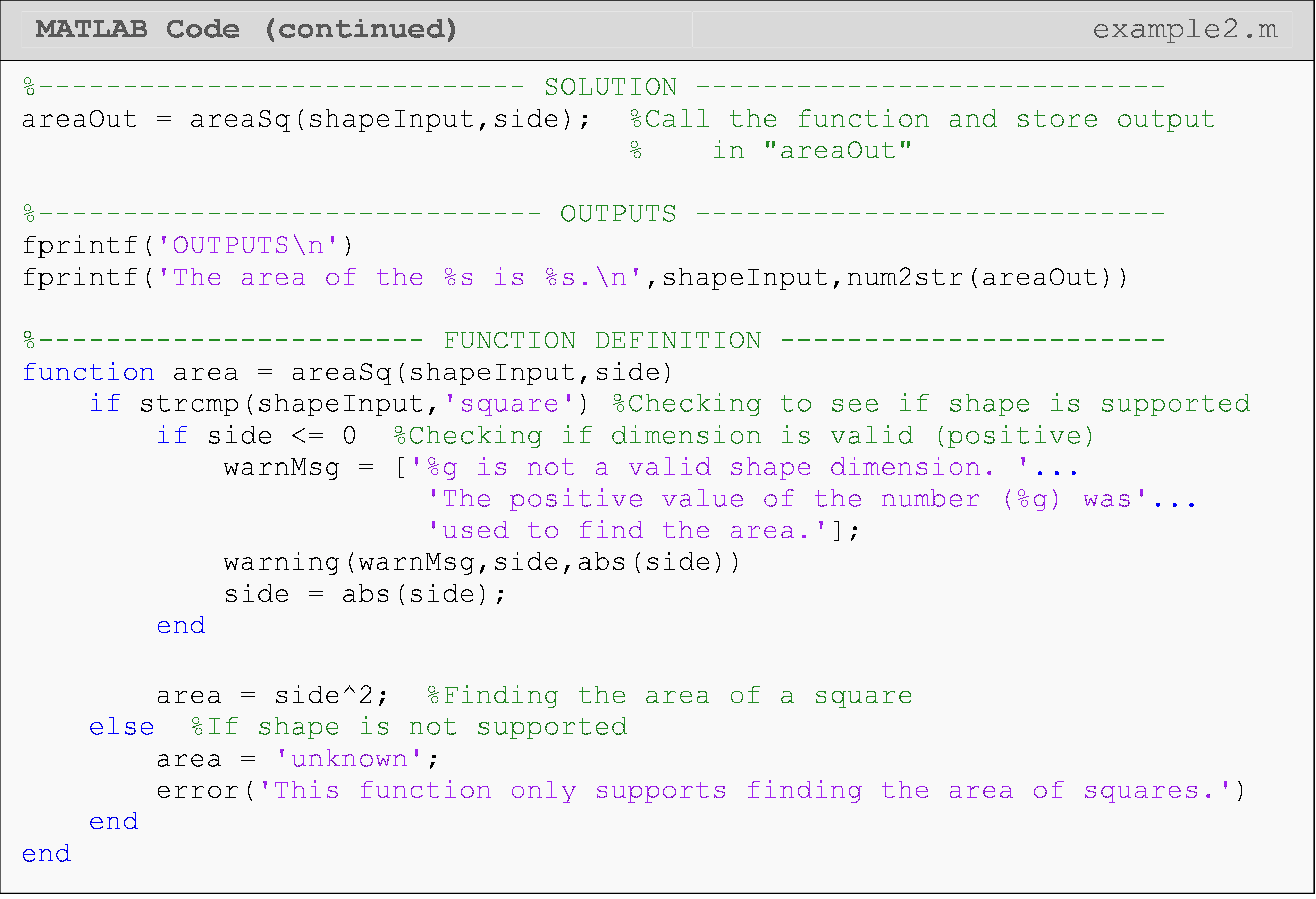
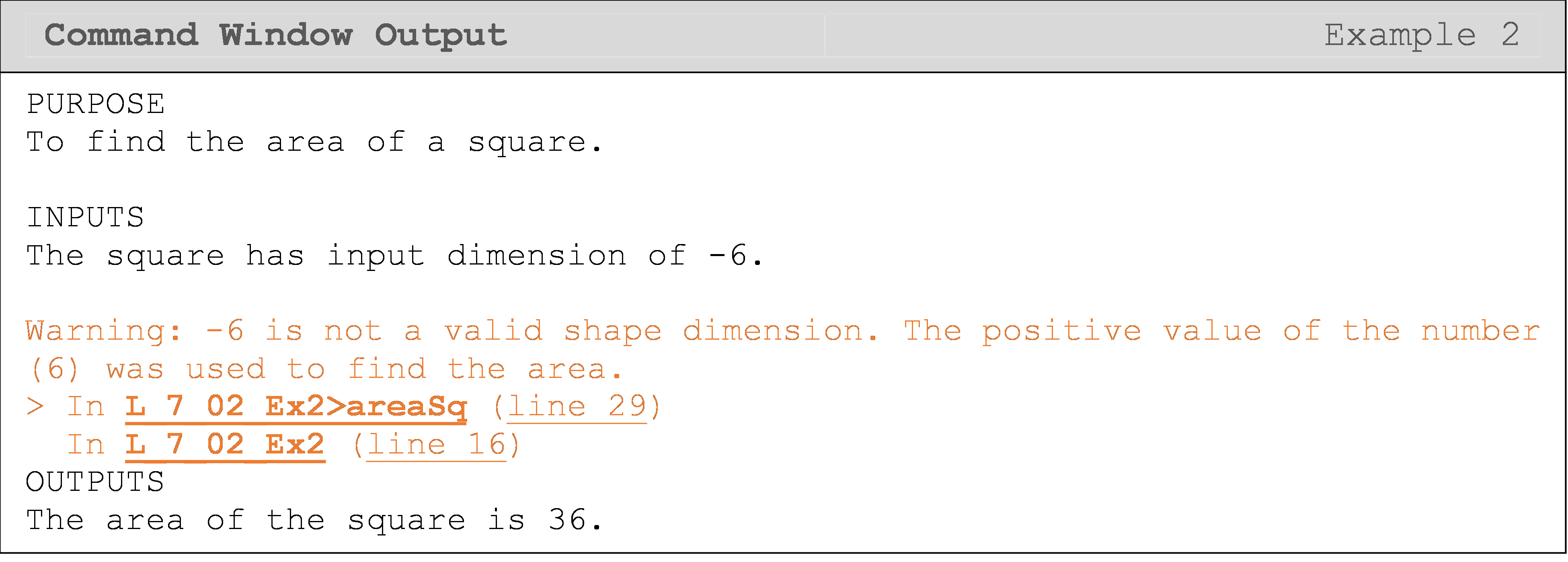
Example 2
Write a function that calculates the area of a square. Inside the function, check that the given dimension of the square is valid and return a warning if it is negative. Also check to see if the input shape is supported and return an error if it is not. In this case, only squares are supported.
Solution

In the following two Command Window outputs, you can see two lines
referenced in each Command Window output. One line is referencing where
the problem (warning/error) occurred in the function (actual cause of
the problem), and the other one is the line where the function is
called. The information given next to the line reference (e.g.,
"L_7_02_Ex2") will help you identify the location of the warning/error
more precisely.
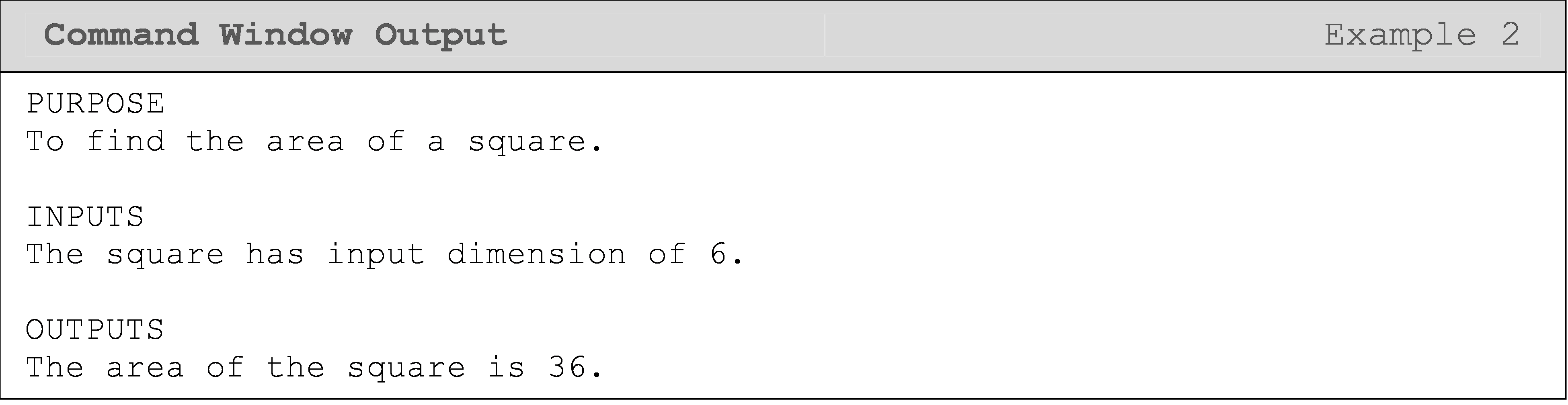
The following Command Window shows the output for the function call
areaSq('circle', 6).
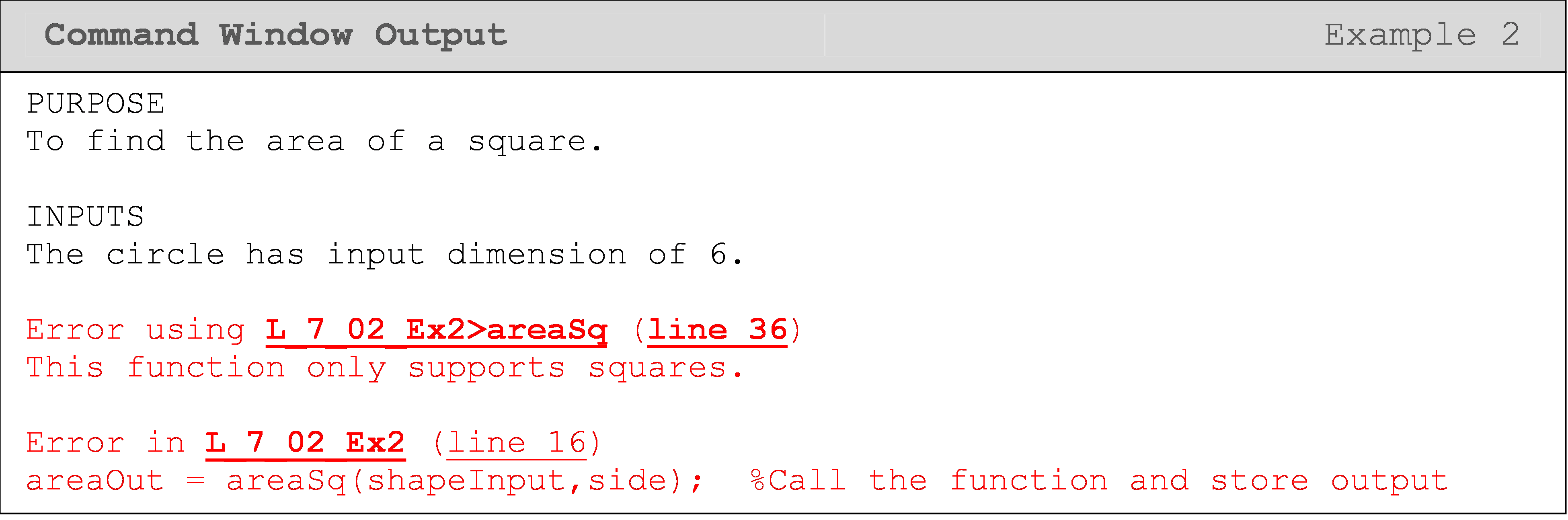
The following Command Window shows the output for the function call
areaSq('square', -6).
Multiple Choice Quiz
(1). For the help command to work for a function, a comment has to be placed
(a) immediately after the function definition line
(b) on the next line after the function definition line
(c) on the last line in the function
(d) anywhere in the function
(2). You are asked to write a function that finds the area of a triangle by using Hero’s formula \({A} = \sqrt{{s}({s} - {a})({s} - {b})({s} - {c})}\) where \({s} = ({a} + {b} + {c})/{2}\) and a, b, and c are the lengths of the sides. When writing an error message in the function, a good case to address would be
(a) a, b, and c are positive
(b) \({s}({s} - {a})({s} - {b})({s} - {c})\) is positive
(c) \({s}({s} - {a})({s} - {b})({s} - {c})\) is negative
(d) s is not an integer
(3). The warning() function accepts inputs of only
(a) static text
(b) text with one variable input
(c) variable inputs
(d) text and/or one or more variable inputs
(4). When an error() statement is enumerated and executed in a function,
it displays
(a) program name
(b) function name
(c) line number
(d) all of the above
(5). When a warning() is triggered,
(a) a custom message is displayed
(b) the program halts
(c) the program pauses until the user continues execution
(d) the program does not show the line number where the warning occurred
Problem Set
(1). Add a description to the function you wrote for Exercise 2 in Lesson 7.1. Give a description of the purpose of the function and a definition of each input and output variable along with what type of data it should contain (e.g., number, string, etc.) and their units when applicable.
(2). Add a description to the function you wrote for Exercise 3 in Lesson 7.1. Give a description of the purpose of the function and a definition of each input and output variable along with what type of data it should contain (e.g., number, string, etc.) and their units when applicable. Add an error message if the user inputs a negative annual percentage rate (APR).
(3). Add a description to the function you wrote for Exercise 6 in Lesson 7.1. Give a description of the purpose of the function and a definition of each input and output variable along with what type of data it should contain (e.g., number, string, etc.) and their units when applicable. Add a warning message if the user inputs a negative income.
(4). Add a description to the function you wrote for Exercise 7 in Lesson 7.1. Give a description of the purpose of the function and a definition of each input and output variable along with what type of data it should contain (e.g., number, string, etc.) and their units when applicable.
Write a MATLAB function that finds the depth to which a metal spherical hollow ball is submerged underwater (see Figure A on the next page), when the density of the metal, the outer radius of the ball, and the thickness of the ball are given. Assume the density of water is 1000 kg/m3. Test your function three times for three different physically acceptable input choices.
Add a description to the function you write. Give a description of the purpose of the function and a definition of each input and output variable along with what type of data it should contain (e.g., number, string, etc.) and their units when applicable.
Hint: Apply the Archimedes’ principle. The volume of the ball underwater for a given depth H is
\[V = \frac{\pi H^{2}\left( 3r_{\text{out}} - H \right)}{3}\]
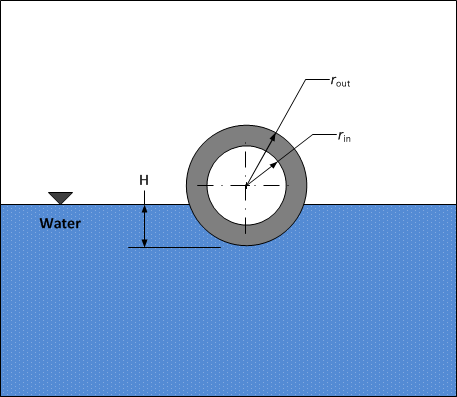
Figure A: Metal ball at equilibrium floating in water.