Module 2: BASIC PROGRAMMING FUNDAMENTALS

Lesson 2.4 – Inputs and Outputs

Learning Objectives

get/store user defined inputs with the input() function,
output messages to the Command Window with disp() and fprintf() functions.

How can I get input from the user?

When a computer programmer hands over a completed program to whoever is going to use it (called the end-user), they typically do not ask the end-user to modify the code. Rather they might prompt the user for the required inputs and then let the program run. The input() function prompts the user in the Command Window to enter a value for a designated variable. The value of this variable will then be used in the program.

Function: Prompts the user for an input.
input()

Function Inputs:
Variable value which is requested, x
String to prompt the user for the variable input, 'the value of x is'

Example Usage:
x = input('the value of x is')

Until the user enters a value for a designated variable in the Command Window, that variable is not defined, and the program will not continue to run. (Note, this is why m-files cannot be published with input() function.) These undefined variables and the pause in the program can cause some troubleshooting issues. If you find that your program is not running properly, check the lower-left corner or the Command Window for the message: 'waiting for input' and assign values as needed. To cancel the program from running altogether, hit Ctrl+c while in the Command Window (while it is the “active” window). The use of the input() function is being shown in Example 2.

How do I display notes in the Command Window?

Like comments in the m-file, displaying information about a program in the Command Window is also important. Information such as the programmer’s name, the purpose of the program and the variables involved in the calculation may be needed to make the output information clear. MATLAB uses several functions to display information in the Command Window. This section will cover the two basic functions that can be used in the m-file to display information in the Command Window. These functions are the disp() and fprintf() functions.

Function: Displays a single string or variable.
disp()

Function Inputs:
Test String, 'Hello', OR, Expression name, x

Example Usage:
disp('Hello')
disp(x)

Example 1

Output the string “The height of the beam is” and the variable height = 12.63 using two separate disp() functions. Then concatenate the given string and variable into a single string and output it using disp().

Solution

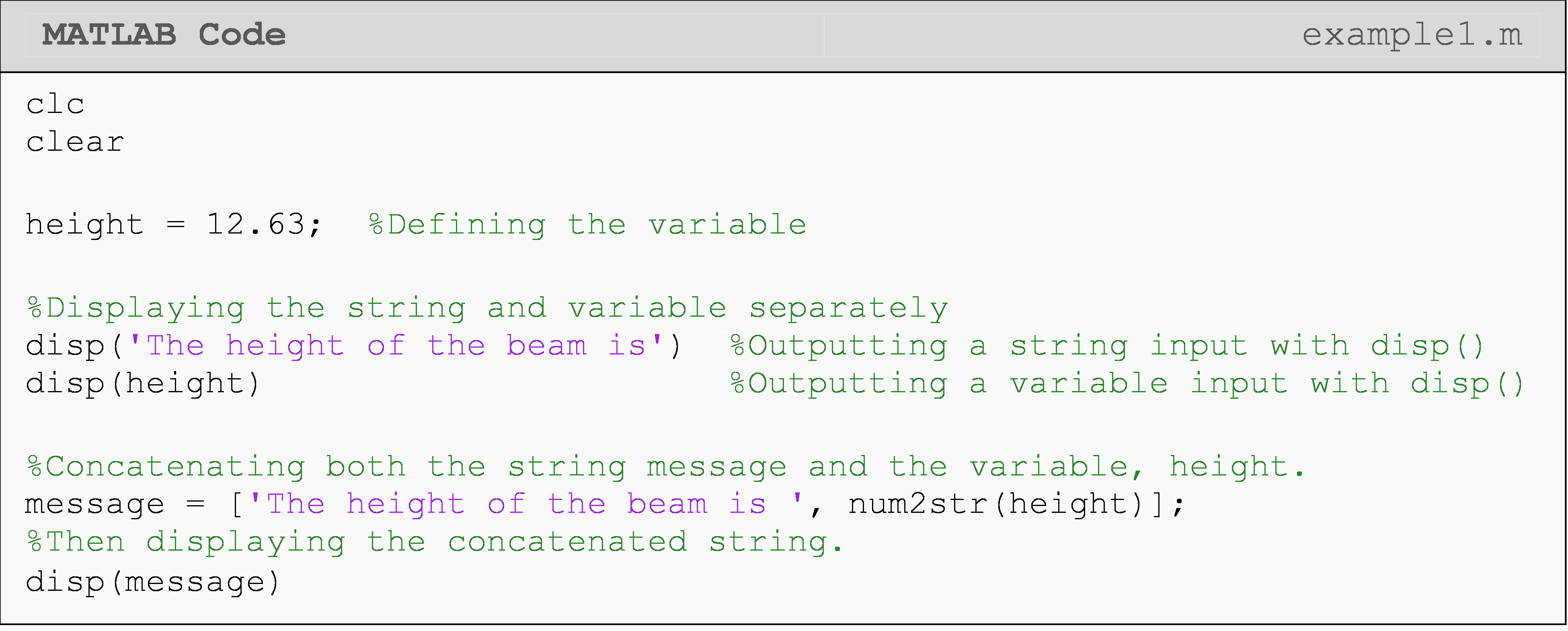
The disp() function displays either a string or a variable in the Command Window. disp() does not require or allow you to manually create new lines. It will do this automatically (see the Command Window output in Example 1). In Example 1, we should several use cases for disp(). Notice that you can output a variable with a message, but it requires you to concatenate them into one string.

Function: Can display from more than one input (both variables and a description).
fprintf()

Function Inputs:
String, 'Note about the number'
Expression name, x (can be more than one)
Conversion character, (%g, %f, %d, etc.)

Example Usage: fprintf('\n note about the number %g \n', x)

The fprintf() function is used to make the Command Window look more organized and easier to follow. The text (string) that is inside the quotes will be displayed to provide a description of a variable, and the %g is where the variable will be placed in the string. The %g, known as a conversion character, sets the display format for the number (e.g., exponential or decimal format) and tells fprintf() what type of data to expect there (e.g., number or string). The fprintf() function does not start a new line to display its information, so we use the \n line character. This line character starts a new line, and the \n is not displayed in the Command Window. The last item one needs to provide for the fprintf() function is the name of the variable to be displayed. Example 2 shows the fprintf()functions being used in an m-file. See Table 1 for commonly used formatting characters that are used inside fprintf().

Table 1: Formats to be used with the fprintf() function.

Task	Formatting Character	Example of Placement
Add a line space (enter key)	`\n`	`fprintf('\n note %g',a)`
Default display	`%g`	`fprintf('\n note %g',a)`
Fixed point display	`%f`	`fprintf('\n note %f',a)`
Single character display	`%c`	`fprintf('\n note %c',a)`
Scientific notation display	`%e`	`fprintf('\n note %e',a)`
String display	`%s`	`fprintf('\n note %s',a)`
Adjust field width (MATLAB controls this automatically)	Any whole number (Using 6 as an example)	`fprintf('\n note %6f',a)`
Adjust precision (change amount of numbers after the decimal point)	Any whole number (Using 2 as an example)	`fprintf('\n note %.2f',a)`

Understanding the correct method for naming and placing variables in the m-file as well as the order in which MATLAB reads these inputs are the core foundations for writing any program in MATLAB. It is very important to make the program as easy for the user or reader as possible. Using the display disp() and fprintf() functions in conjunction with the suppression character (;) and clc command is vital. These functions provide a good foundation for any m-file.

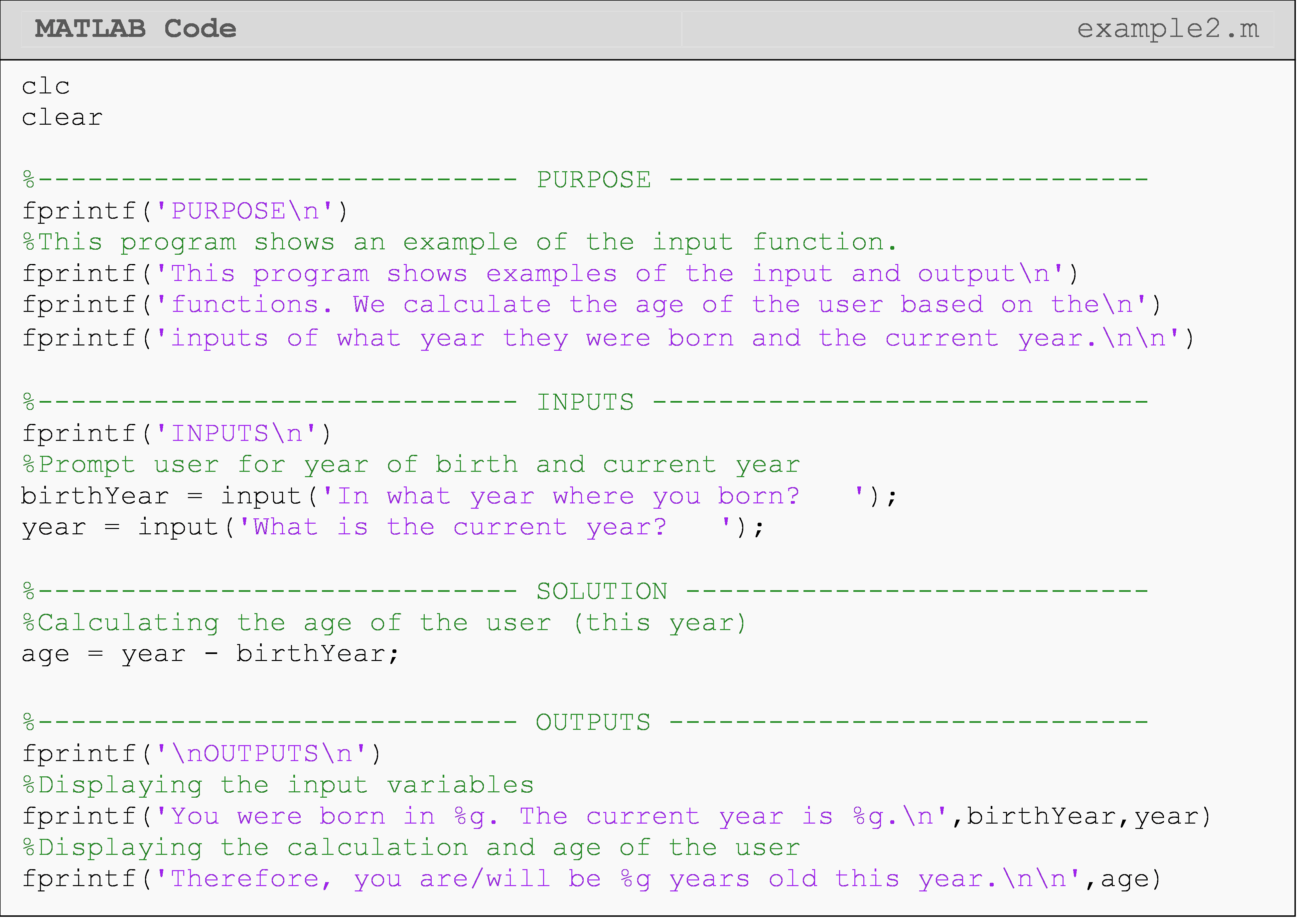
Example 2 shows the input(), disp(), and fprintf() functions being used together in a single program. The usage of each character is shown with a generic fprintf() function call. Table 1 shows other formatting characters that are commonly used with the fprintf() function.

Example 2

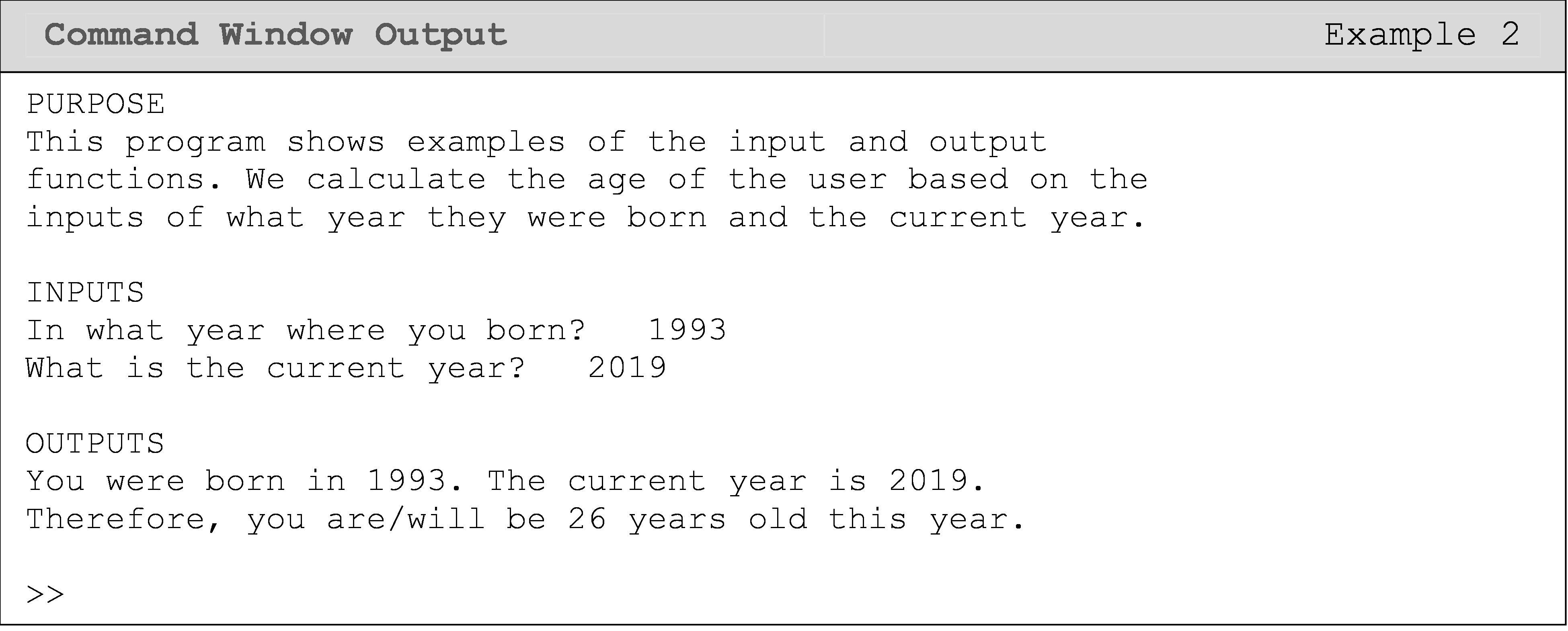
Calculate the age of the user based on the inputs of what year they were born and the current year. Output the inputs (birth and current years) and the result (age) in the Command Window with a description of the numbers.

Solution

The Command Window output for Example 2 is shown below, which after the user entered the desired input.

Lesson Summary of New Syntax and Programming Tools

Task	Syntax	Example Usage
Ask the user for an input	`input()`	`input('What is your age?')`
Display a note in the Command Window	`disp()`	`disp('note')`
Display a variable with a note in the Command Window	`fprintf()`	`fprintf('note %g',a)`

Multiple Choice Quiz

(1). To display, Question 2, in the Command Window, the correct syntax is

(a) disp(Question 2)

(b) display('Question 2')

(d) Question 2

(2). Although not typically necessary, one can use which of the following to add a new blank line?

(a) disp(' ')

(b) disp('\n')

(d) disp()

(3). What is the output of the following code? Assume the user inputs the number 10 when prompted.

(a) pressure = 2

(b) pressure = 2.0

(d) 0.5

(4). The correct fprintf() usage to display the variable myString = 'strings are fun' is

(a) fprintf('I think %s, but they do not agree!\n')

(b) fprintf('I think %.3f, but they do not!\n')

(d) fprintf('I think %s, but they do not!\n',myString)

(5). To output the variable length = 8.40235 with two decimal places, use

(a) fprintf('The length is %g\n',length)

(b) fprintf('The length is %2d\n',length)

(d) fprintf('The length is %.2f\n',length)

Problem Set

(1). Print out the following string in the Command Window using fprintf().

cm1 = 'My goal is to become an engineer.'

(2). Find the product of any two numbers by using input() to prompt the user to enter the numbers in the Command Window. Use fprintf() to display the product of the numbers in the Command Window.

(3). Find and output in the Command Window the kinetic energy of an object of mass, m traveling at a specified instantaneous velocity, v. Use the input() function to prompt the user to enter the values of the mass (kg) and velocity (m/s).

Use fprintf() to display the numeric value of the kinetic energy (J) of the object. Be sure to add a good description for the input() and fprintf() functions to avoid any miscommunications (that is, display the units as well). Hint: The formula for kinetic energy is \[\text{KE} = \frac{1}{2}mv^{2}\].

(4). Write a program in MATLAB that outputs the maximum tensile normal force that a steel cylindrical tube can handle without breaking. A factor of safety n and inner and outer diameters (meters) of the tube are specified by the user. The fprintf() function must be used where needed for a detailed description. The other specifications and formulas are given below.

\[{\sigma_{\text{steel}} = 245 \times 10^{6}\text{Pa,}}\] \[{\sigma_{\text{Safe}} = \frac{\sigma_{\text{steel}}}{n},}\] \[{F_{\text{Safe}} = \text{Area}\left( \sigma_{\text{Safe}} \right),}\] \[{\text{Area} = \frac{1}{4}\pi\left( \left( D_{\text{outer}} \right)^{2} - \left( D_{\text{inner}} \right)^{2} \right).}\]

where,

$D_{inner}$ is the inner diameter (m) of the tube,

$D_{outer}$ is the outer diameter (m) of the tube,

$\sigma_{\text{steel}}$ is the yield strength of steel (does not require the input() function).

(5). The monthly payment on a car loan is given by the formula

\[\displaystyle PMT = \frac{LA*IPM}{1 - (1 + IPM)^{- NM}}\]

where,

PMT = monthly payment in dollars,

LA = loan amount in dollars,

IPM = interest rate given as a fraction per month (Note the units),

NM = number of monthly payments (Note the units).

Write a MATLAB program that calculates the monthly payment for buying a car, based on the loan amount (dollars), length of the loan (years) and interest rate (annual percentage rate). Three inputs are assigned at the beginning of the worksheet through a variable assignment:

Loan amount entered in dollars, LA
Length of loan entered in integer years, NY, and
Interest rate entered in annual percentage rate (APR), APR.

The output is:

The monthly payment on the car.

Display and print with an explanation at least the following in the Command Window.

A short description of the problem,
Loan amount in dollars,
Length of loan in integer years,
Interest rate in annual percentage rate,
Monthly payment in dollars.

Example to compare our MATLAB program against:

For a loan of $14,800 at 6.75% annual percentage rate (APR) for a 4 year term,

$LA = \$14,800$

$IPM= APR/(12*100)=6.75/(12*100) = 0.005625$

$NM = NY * 12 = 4 * 12= 48 \text{ months}$

Hence,

$\displaystyle PMT = \frac{14800*0.005625}{1 - (1 + 0.005625)^{- 48}}$

= $352.69