Module 4: MATH AND DATA ANALYSIS
Learning Objectives
After reading this lesson, you should be able to:
integrate a continuous function in MATLAB,
integrate a discrete function in MATLAB.
What is integration?
Integration is defined as the area under a curve (see Figure 1).
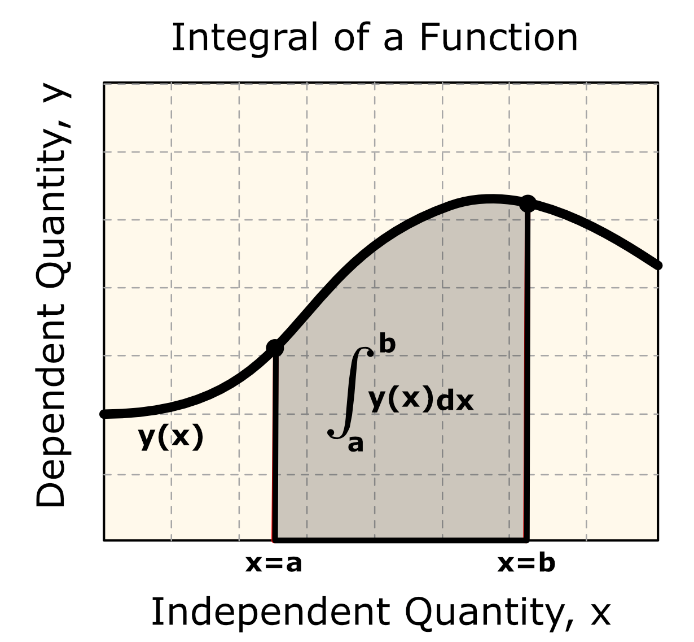
Figure 1: The integral of the function \(y(x)\) from the limits of a
to b is shown in the shaded area under the curve.
Why would we want to integrate a function? Among the most common examples are finding the velocity of a body from an acceleration function and displacement of a body from a velocity function. Throughout many engineering fields, there are countless applications for integral calculus. Sometimes, these integrals cannot be found exactly.
The general form of an integral is given by
\[I = \int_{a}^{b}{f(x)dx}\]
where,
\(f(x)\) is called the integrand,
\(a =\) lower limit of integration,
\(b =\) upper limit of integration
As you can see from Equation (1), we need four inputs to conduct integration.
The function \(f(x)\) that needs to be integrated.
The variable with respect to which the function needs to be integrated x.
The lower limit of integration a.
The upper limit of integration b.
The type of integral that requires all four of these inputs is called a definite integral. In contrast, the indefinite integral only requires the first two inputs: the function \(f(x)\) and the variable x. MATLAB can conduct both types of integration.
How does MATLAB conduct symbolic integration?
While using MATLAB, several integration functions are available to the
programmer. Depending on the type of integration required, the two main
functions are the int() and trapz(). The int() function is used for
integrating continuous functions (both indefinite and definite), whereas
the trapz() function is used when integrating a discrete function.
Both of these functions will be discussed in this lesson.
Recall from your integral calculus class that when conducting indefinite
integration, a constant (usually “C”) must be added to the solution.
Look at Example 1 to see the int() function in use.
Important Note: MATLAB does not automatically add a constant of integration for an indefinite integral.
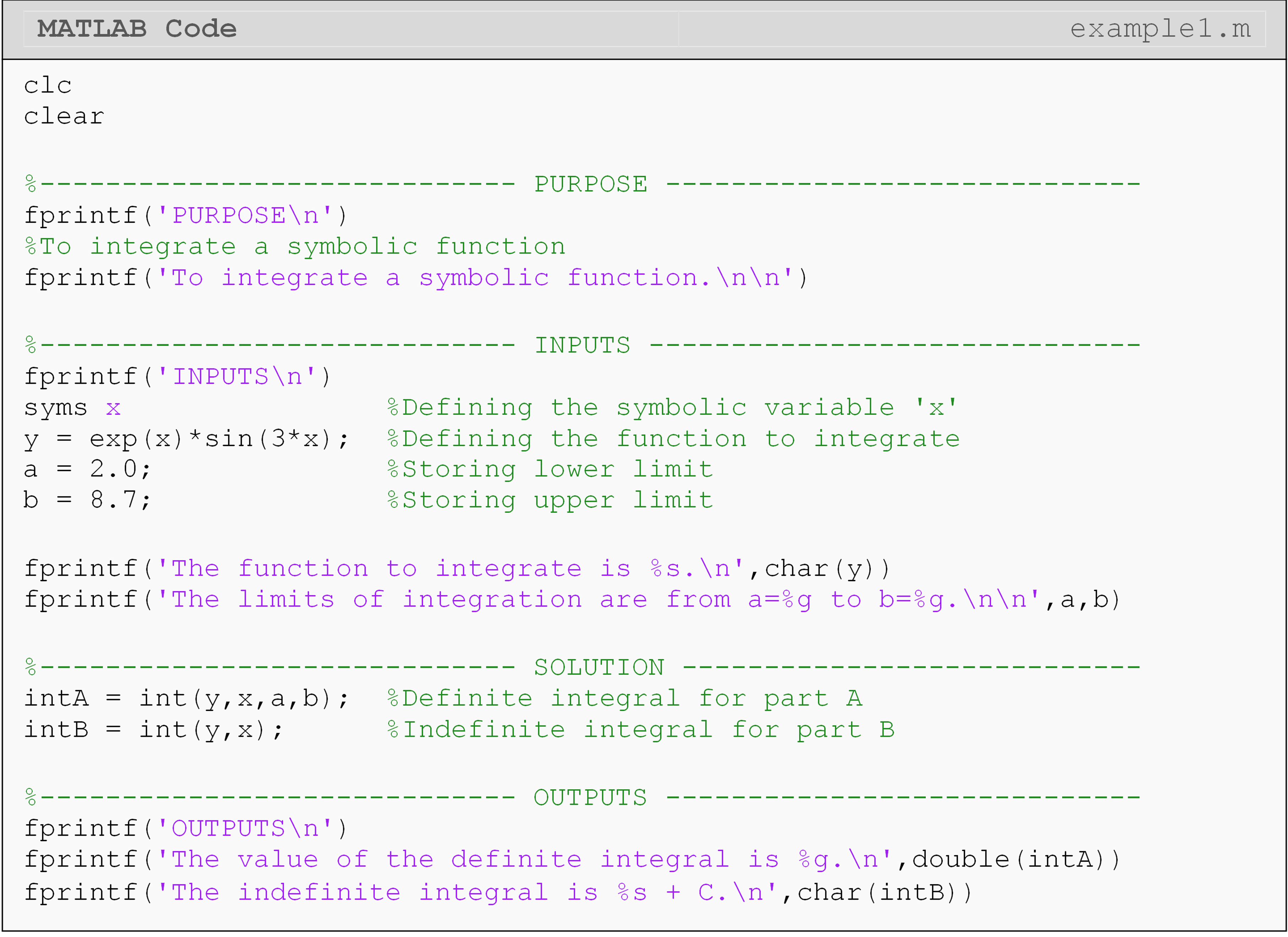
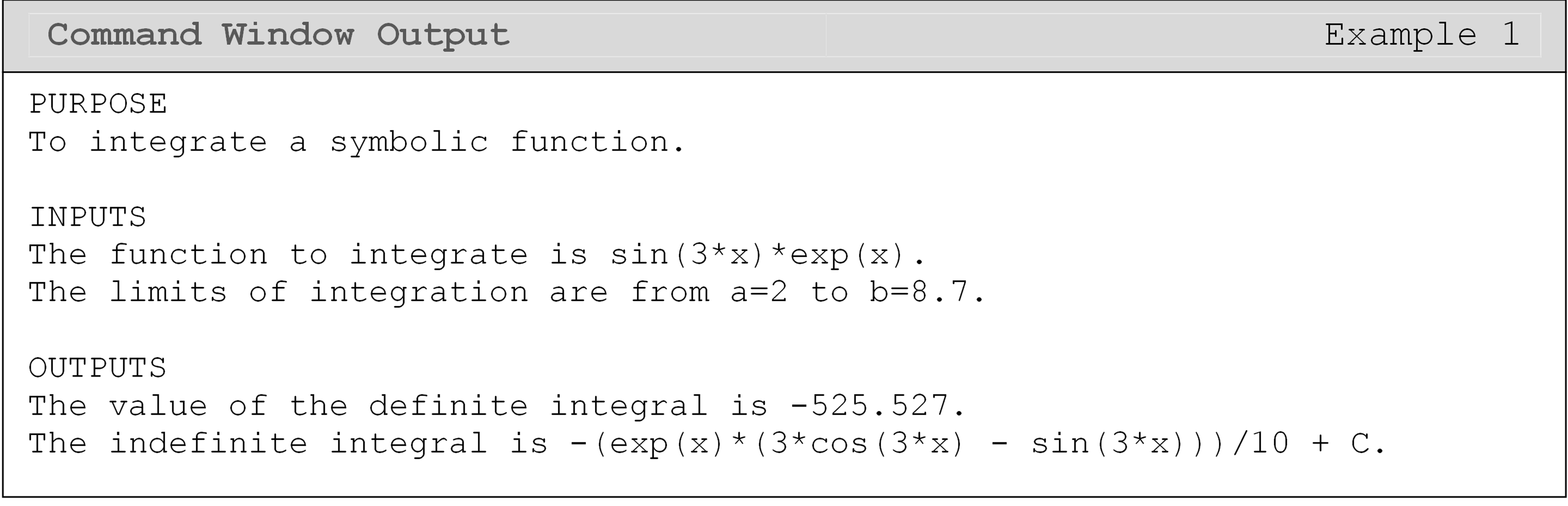
Example 1
Use the int() function to evaluate the integrals in parts (a) and (b).
Evaluate both integrals in the same m-file, and use the fprintf() or
disp() function to display the outputs in the Command Window.
\(\int_{2.0}^{8.7}{e^{x}\sin(3x)dx}\)
\(\int_{}^{}{e^{x}\sin(3x)dx}\)
Solution
We will use the int() function to evaluate both integrals. For part
(a) there will be four inputs to the function, and in part (b) we will
need two inputs. Notice that the syms command must be used before the
int() function in the m-file to establish the symbolic variables in
the integrand. Because the integral in part (b) is indefinite, the “+ C”
was added to output the most appropriate solution.
Can MATLAB do numerical integration of discrete functions?
As mentioned previously, the trapz() function is used when the
integrand is given as discrete data points. An example of when to use
the trapz() function is to integrate a function y given at discrete
x-values.
The trapz() function uses numerical integration to find the area under
a given curve. It joins consecutive data points via straight lines.
Using this line and the horizontal axis, a trapezoidal segment (shape)
is formed. To do this, the two vectors x and y to be evaluated must
be the same size. For example, 10 data pairs would create 9 trapezoids.
The summation of the area of these trapezoids is estimated as the value
of the integral. This math behind the numerical method is not required
to use trapz(), as the inputs are simply two vectors, but it is
important to understand for any real-world application of the method.
Example 2 shows the use of the trapz() function.
Important Note:
trapz(x,y)approximates the integral frommin(x)tomax(x).
Example 2
Input the x and y data into a new MATLAB m-file.
Table 1: Data pairs to be used for Example 2.
| x | y |
|---|---|
| 0 | 2.01 |
| 1 | 3.97 |
| 3 | 20.2 |
| 5 | 50.95 |
| 6 | 72.76 |
| 9 | 166.5 |
Plot y vs. x on a standard linear plot where y is the vertical
axis and x is the horizontal axis. Use the trapz() function to find
the area under the curve from x = 0 to x = 9. Output the resulting
value using the fprintf() function to the Command Window.
Solution
Because the data provided is a discrete function, the trapz() function
will be used for the integration. Remember, in order for the trapz()
function to work, the two data arrays must be the same size. In this
case, the two vectors both have 6 elements.
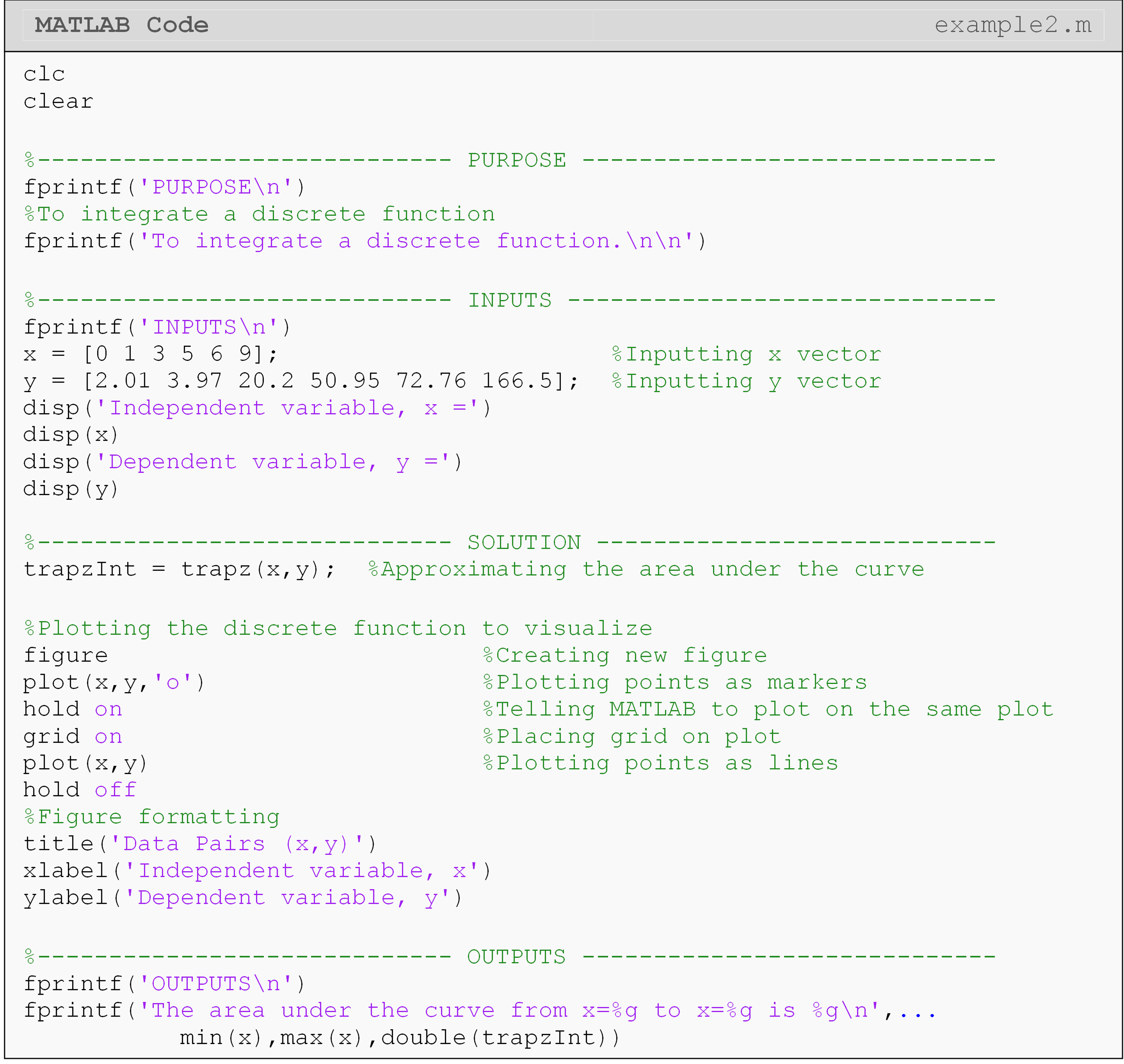
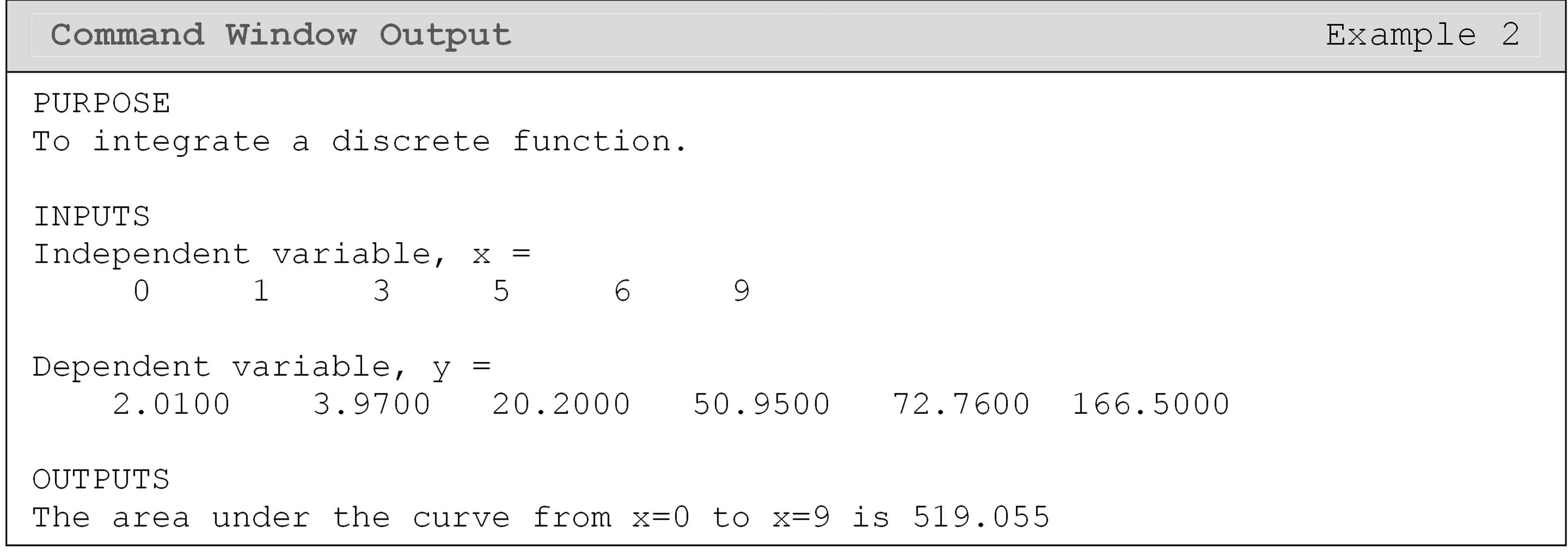
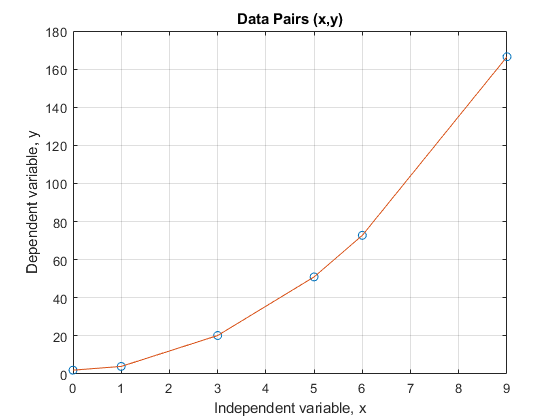
Figure 2: Figure of plotted points for Example 2.
Lesson Summary of New Syntax and Programming Tools
| Task | Syntax | Example Usage |
|---|---|---|
| Definite integral of a symbolic function | int() |
int(y,x,a,b) |
| Indefinite integral of a symbolic function | int() |
int(y,x) |
| Approximate the area under a curve given by discrete data points | trapz() |
trapz(x,y) |
Multiple Choice Quiz
(1). The MATLAB function for integration of a symbolic function is
(a) integrate()
(b) diff()
(c) integ()
(d) int()
(2). The output of trapz() is
(a) a mathematical function that is best fit to the given data.
(b) a single number that is the approximate area under the curve.
(c) a symbolic function that is the integral of the input discrete function.
(d) a vector of values.
(3). To find \(\int_{4}^{8}{7e^{- 4x}dx}\), the correct line of code to add to the following program is
(a) int(7\*exp(-4\*x),x,4,8)
(b) int(7\*exp(-4\*x),x,8,4)
(c) int(7exp\^(-4\*x),x,4,8)
(d) int(7exp(-4x),x,4,8)
(4). To find\(\int_{12}^{8}{(x^{2} + 2)dx}\), the correct line of code to add to the following program is
(a) int(x\^2+2,x,8,12)
(b) int(x\*\*2,x,8,12)
(c) int(x\^2+2,x,12,8)
(d) int(x\^2+2,x,8,12)
(5). To numerically integrate a discrete function, y calculated as a function of x from x = 1 to x = 10 using trapezoidal segments, the correct line of code to add to the following program is
(a) trapz(x,y,1,10)
(b) trapz(y,x,1,10)
(c) trapz(x,y)
(d) trapz(y,x)
Problem Set
Note: In these exercises, if a vector is raised to a power, remember to
use the (.) operator. For example, if you want to square each element of
a vector vec, you will do this by using vec.^2. Similarly, if you
want to find the reciprocal of each element of the vector vec, you
will do this by using 1/.vec.We took similar measures before when
plotting in Module 3. The full explanation for this procedure is
contained in the next lesson (Lesson 4.6).
(1). Use the int() function to find \(\int_{2}^{8}{e^{4x}\cos(x)dx}\)
(2). Use the int() function to find\(\int_{3.4}^{8.2}{f(x)dx}\)
where
\[f(x) = \left\{ \begin{matrix} \& x^{2},\text{\ \ \ }0 \leq x < 4, \\ \& x^{3},\text{\ \ \ }4 \leq x < 10. \\ \end{matrix} \right.\ \]
(3). Find the vertical distance covered by a rocket from \(t = 8\) to \(t = 30\) seconds by solving the integral below.
\[x = \int_{8}^{30}{\left( 2000\ln\left\lbrack \frac{140000}{140000 - 2100t} \right\rbrack - 9.8t \right)dt}\]
(4). A company advertises that every roll of toilet paper has at least 250 sheets. The probability that there are 250 or more sheets in the toilet paper is given by
\[P(y \geq 250) = \int_{250}^{\infty}{0.3515e^{- 0.3881\text{\ \ }(y - 252.2)^{\text{\ \ }2}}dy}.\]
Find the value of the integral (thus finding the probability) using the
int() function.
(5). Use the trapz() function to find \(\int_{1.2}^{8.6}{zdz}\), given
\[z = \ln\left( r^{2} \right)r\]
(6). A trunnion of diameter \(12.363^{''}\) has to be cooled from a room temperature of \(80{^\circ}F\) before it is shrink-fitted into a steel hub (Figure A).

Figure A: The hub and trunnion prior to shrink fitting.
The equation that gives the diametric contraction (in inches) of the trunnion by immersing it in a dry-ice/alcohol (temperature is \(- 108{^\circ}F\)) mixture is given by
\[\Delta D = 12.363\int_{80}^{- 108}{\left( - 1.2278 \times 10^{- 11}T^{2} + 6.1946 \times 10^{- 9}T + 6.015 \times 10^{- 6} \right)dT}\]
Use int() function to find the diametric contraction of the trunnion
and the new trunnion diameter. Output the program results to the Command
Window with a brief description.
(7). Find \(\int_{3.1}^{8.5}{(x^{3} - 4x^{2} + 7x)dx}\) using both the
trapz() and int() functions. Compare the outputs in the Command
Window using fprintf() function. Show at least 6 decimal places for
all outputs.
(8). Given the following (x, y) data
(3, 2), (5.4, 4.6), (6.2, 5.1), (7.9, 6.7), (11.0, 8.5), (15.7, 14.0)
Use trapz() function to find \(\int_{3}^{15.7}{ydx}\).
(9). The error function is defined as \(erf(y) = \frac{2}{\sqrt{\pi}}\int_{0}^{y}{e^{- z}}^{2}dz\).
Using a single m-file find the values of erf(0.2), erf (0.5), and
erf (3.4). Compare these three results to the MATLAB output for the
error function erf(). Use the fprintf() function to compare and
output the results.